추천 시스템에서 가장 흔히 사용되는 Matrix Factorization은 Rating matrix $R$을 두 매트릭스 $(U ,V)$로 factorize한다. Matrix Factorization에 대해서는 블로그의 설명이 상당히 자세히 되어 있다. 그러니까, 요약하자면, 유저의 예상 평점을 맞추는 문제는 Rating matrix를 잘 Reconstruct하는
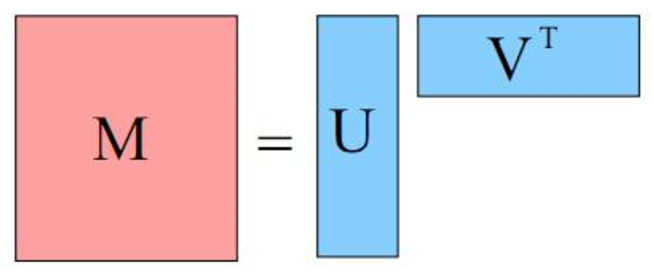
가 되는 좋은 \(U\)와 \(V\)를 찾는 문제로 바꿀 수 있다. 이는
\[L(U,V) = \sum_{u,i}{(R_{u,i} - u_u^Tv_i)}\]이 Loss function \(L(U,V)\)을 최소화하는 걸로 바꿀 수 있다. (사실 이건, 주어진 데이터에 대한 Gaussian Prior를 갖는 model의 MLE를 구하는 과정으로 볼 수 있다.) 이에 대해서는 기회가 될 때 더 자세히 적는 게 좋은 것 같다. (내 짧은 공부로는) 사실 대체로 Machine Learning에서 사용하는 많은 모델은 Bayesian MLE/MAP approximation이다.
Gradient Descent Method (GD)
Loss function을 minimize하는 방법은 가장 대표적으로 Gradient Descent방법이 있다. 이는 현재 Machine Learning, Optimization 분야에서 가장 많이 사용되는 방법이다. 많은 상황에서 \(f(x)\)를 충분히 작게 하는 \(x\)을 잘 찾는다고 알려져 있다.
Gradient Descent 방법의 가장 큰 장점은, 임의의 미분 가능한 함수를 충분히 작게 만드는 값을 찾는(앞으로 최소값을 찾는다고 표현하겠다. 하지만, 실제로는 최소값이 아니라, Local minima를 찾는다.) 일을 할 수 있다는 점이다. 복잡한 함수에 대해서도, 미분이 가능하다면 꽤 그럴싸한 답을 찾아낸다. 단점으로는
- Optimal solution을 찾지 않는 Greedy한 방법이라는 점.
- Training 시간이 비교적 길다는 점.
같은 점이 존재한다. 다만, Matrix Factorization이나, 여러 Convex Optimization에 사용되는 특별한 form을 제외하면, 일반해를 간단하게 구하는 방법이 그리 많지 않기 때문에 특히 딥 러닝에서 자주 사용되는 방법이다.
Alternating Least Squares (ALS)
위에서 언급했듯이 Gradient Descent 방법은 일반적으로 상당히 느리다. 몇몇 특수한 형태(주로 Convex)의 문제는, 더욱 간단한 방법으로 문제를 해결할 수 있다. Matrix Factorization problem에서도 간단하게 문제를 Solving하는 방법이 존재한다.
Matrix Factorization 방법에서 최소값을 찾고자 하는 값은 비교적 간단하고, 아름답다.
주어진 로스 함수는 user vector \(u\)와 item vector \(v\) 의 Quadratic form으로 나타낼 수 있다. 고등학교 수학 시간에 배웠던 것 같은데, 2차함수는 항상 최소값을 갖는다. 2차함수 \(f(x)\) 의 최소값은 \(x'\) 가 \(f(x') \text{where }f(x')'= 0\) 을 만족시키는 값에서이다.
\[\begin{eqnarray} L(U,V) = \sum_{u,i}{(R_{u,i} - u_u^Tv_i)^{2}} \\ = \end{eqnarray}\]이 Loss function \(L(U,V)\)을 \(u_{u}\)에 대해 미분하면, \(\frac{\partial }{\partial u_{u}} L(U,V) = \sum_{u,i AAA }(R_{u,i} - u_u^Tv_i)(-v_i)\)
V가 변하지 않는다고 가정하면 loss function은 \(L(u_u)\)이라 볼 수 있다. (변수가 \(u_u\) 하나뿐인 식으로 볼 수 있다.) 아까 고등학교 수학 얘기를 왜 했냐면… 이 \(L(u_u)\)는 \(u_u\)에 대한 이차함수이고, 이 함수가 최소일 때는 \(\frac{d}{d u_{u}} L(u_u) = 0\)가 0일 때이다. \(U\) 혹은 \(V\)가 singular가 아니라면, 이를 만족하는 최소값 \(u_u\)를 항상 구할 수 있다.
ALS의 메인 아이디어는, 꽤나 복잡한 Quadratic form의 loss function을, 변수 하나를 고정시키면 쉽게(빠르게) 해를 구할 수 있다는 것이다. 원문 링크
이런 coordinate update methods는 꽤 널리 사용되고 있다고 한다. (나중에 더 알게 된 건데, Spark MlLib이나 현재 product가 제공하는 추천 솔루션들은 대부분 이 ALS를 이용해 matrix factorization을 포함하고 있다.)
필요한 것만 가볍게 얘기하는 벡터 미분
- 벡터를 한 변수(scalar, 예를들면 \(x\))에 대해 편미분하는 건, 벡터의 모든 원소를 각각 그 변수에 미분하는 것이다.
ex)
\(v = [f(x),g(x),h(x)]^T\) 이면, \(\frac{\partial}{\partial x}v = [\frac{\partial}{\partial x}f(x),\frac{\partial}{\partial x}g(x),\frac{\partial}{\partial x}h(x)]^T\)
- scalar를 한 vector에 대해 편미분하는 건, scalar를 벡터의 각 element에 미분하는 것이다.
ex)
\(v = [v_1,v_2,v_3]^T\)이고, \(f(v) = \sum_{i} v_{i}^2\)이면, \(\frac{\partial}{\partial v}f(v) = [2v_1,2v_2,2v_3]^T\)이다.
더 자세한 규칙에 대해서는 Kamper의 Vector and Matrix Calculus을 참고. 이런 걸 기억하고 있으면 좋을 텐데 보통 다른 그때그때 유도하거나, 이런 sheet를 찾거나 한다. 자주 쓰는 벡터/매트릭스 미분에 대해서는 외워지지만 역시 잘 되지 않는다.
\(L(U,V)\)을 \(v_{i}\)에 대해 미분하면 다음과 같은 식이 나온다.
\[\frac{\partial }{\partial u_{u}} L(U,V) = \sum_{u,i \text{where ...} }(R_{u,i} - u_u^Tv_i)(-{v_i}^T)\]\(\frac{\partial }{\partial u_{u}} L(U,V) = 0\)이 되는 지점의 \(u_u\)가 우리가 찾는 해가 된다. 시그마 밑의 조건이 조금 복잡한데…
\[\begin{eqnarray} \sum_{}{(R_{ui} - u_u^Tv_i)}(-v_i) \\ u_u^T(\sum_{}{v_iv_i^T} = \sum_{}{R_{ui}v_i^T}) \\ u_u^T = (\sum_{}{R_{ui}v_i^T})(\sum_{}{v_iv_i^T})^{-1} \\ u_u = (\sum_{}{v_iv_i^T})^{-1}(\sum_{}{R_{ui}v_i}) \text{or} \\ (\sum_{}{v_iv_i^T})u_i = (\sum_{}{R_{ui}v_i}) \end{eqnarray}\]Paramter $u_u$의 update는 \(Ax=b\) 꼴의 linear equation을 푸는 것과 같다는 것을 눈치챘을 것이다(실제로도 같다.). 또한, parameter $u_{u1}$을 업데이트하는 것과 parameter$u_{u2}$의 업데이트는 서로 겹치지 않으므로, parallelize 또한 쉽다는 사실을 알아챌 수 있을 것이다.
마찬가지로 아이템의 vector representation $v_i$의 업데이트 또한 같은 방법으로 구할 수 있다.
\[v_i = (\sum_{}{u_uu_u^T})^{-1}(\sum_{}{R_{ui}u_u}) \text{or} \\ (\sum_{}{u_uu_u^T})v_i = (\sum_{}{R_{ui}u_u})\]예상 평점을 실제로 구할때는 단순히 \(\hat{R_{ui}} = u_u^Tv_i\)가 아니라
\[\begin{eqnarray} \hat{R_{ui}} = u_u^Tv_i + b_u + b_i + mu \\ \text{where} b_u \text{is bias for user } u, b_i \text{is bias for item } i,\text{and } \mu \text{global mean rating (in the training dataset)}. \end{eqnarray}\]으로 예상 평점을 예측한다. implcit feedback의 경우에는 유저와 아이템의 bias를 잘 사용하지 않는다. 다만, negative feedback의 importance를 고려해 objective function을
\[L := \sum_{u,i}{c_{ui}(y_{ui} - u_u^Tv_i)^2}\]\(y_{ui}\)가 1보다 큰 값일 때의 \(c_{ui}보다\)y_{ui}\(가 0일 때의\)c_{ui}$$를 더 크게 하는 modification이 있다.
- 실제 구현된 biasedMF 모델의 두 implemetnation의 비교 결과 구현 : github