Logistic Matrix Factorization and Negative Sampling

잡담

카카오에서 영입 제의를 받았다(예이!!). 근데 내가 미필이라 어떻게 될 지 모르겠다(ㅠㅠ)

(내 생각에) 요즘 추천 시스템은 Implicit feedback을 어떻게 해석하는가에 관한 문제인 것 같다. 솔직히 어떻게 해석해야 좋은지 잘 모르겠다. 이를 확률인 $p(l_{ui} \vert \theta)$로 보는게 가장 좋을 것 같긴 한데, WMF는 확률적 해석을 하지 않는, Regression이다.(WMF에 관한 내용은 다른 글, 혹은 내 블로그 포스트을 봐도…)

“유저가 어떤 아이템을 좋아하는 것을 regression으로 해결하는 것이 좋은 일인가”에 대해 조금 답답한 점이 있었는데, 이를 확률적으로 표현한 뒤 해결하는 방법이 있는지 찾아보다, logistic matrix factorization이라는 논문을 알게 되었다.

Logistic Matrix Factorization

이 글을 읽는 사람은 기본적인 CF, Matrix Factorization에 대해 잘 알고 있다고 가정한다.

Logistic Matrix Factorization은 User $u$와 Item $i$가 interaction할 확률을 모델링하는 Matrix Factorization 모델이다. 또한 이를 이용해 user $u$가 item $i$와 interact한다는 사건을 확률적으로 표현할 수 있게 되었다. 즉, 간단히 말해 유저가 어떤 아이템을 좋아할 확률을 다음과 같이 표현하겠다는 얘기이다.

유저와 아이템의 interaction을 일반적인 matrix factorization과는 다르게 sigmoid 함수를 이용해 표현하는 점 이 모델의 독특한 점이다. 즉, user $u$가 item $i$와 interaction할 확률은 모델링하며, 이는 다음과 같이 표현된다.

where $l_ui$ is the event the user $u$ interacts with the item $i$, $x_u$, $y_i$ are latent representation for user $u$, and item $i$. $b_u$, $b_i$ are usre, item bias, respectively.

bias term의 해석

어떤 아이템은 많은 유저와의 interaction이 존재한다. 즉, popular한 아이템일 경우 bias의 값이 높다고 해석할 수 있다. 어떤 유저는 많은 아이템과 interaction했다.Popularity bias를 bias term이 해결할 것이라 기대하며 이런 Bias term을 추가한 것 같다.

Likelihood function

일반적으로, Logistic Regression과 같은 문제에서는 예측하려는 사건 $y_i$가 Bernoulli 분포를 따른다고 가정한다. 즉 $y_i$는 0 또는 1이다. 또한 likelihood는 다음과 같은 형태를 띄게 된다.

근데, 이 논문에서는 왜인지 likelihood를 다음과 같이 정의했다.

$c_i$는 (WMF에도 존재하는)Confidence Term이다.

이게 어떤 분포의 likelihood인지 조금 생각을 해 봤는데, $y_i$는 $\text{Beta}(c_i+1, 2)$ 분포를 따르게 되는 것 같다. 베타 분포는 값이 0과 1 사이에 존재하는 분포이다.

왜 이렇게 정의한지 잘 이해가 가지 않는다. 아무튼 이런 식으로 유저가 아이템을 좋아할 만한 사건을 정의하면, $y_i$는 “유저가 아이템을 좋아한다”는 사건이 아니라, “유저가 아이템을 좋아하는 정도”이며, 이는 0과 1사이의 값을 갖는다는 식으로 생각할 수 있다.

$y_i$를 유저 $u$가 아이템 $i$를 좋아하는 정도 $l_{ui}$로 바꿔 likelihood를 다시 한 번 표현해 보면 다음과 같다.

where $X = [x_1, x_2, \cdots], Y = [y_1, y_2, \cdots], B_u = [b_{u1}, \cdots], B_i = [b_{i1}, \cdots]$

likelihood에 log를 취한 후에, X, Y에 L2 regularization을 더해 주면 모델의 objective를 유도할 수 있다.

where $r_{ui} = x_u^Ty_i + b_u+b_i$

$\sigma_u$와 $\sigma_i$를 $\lambda$로 놓고, $x_u$에 대해 gradient를 구하면 다음과 같다.

$b_u$에 대한 gradient도 비슷하다.

($y_i$, $b_i$에 대한 gradient는 대칭적이므로 생략한다)

모델의 Objective를 정의하고 gradient를 계산했으면 모델을 실제로 트레이닝할 수 있다. 하지만 이 모델에는 심각한 단점이 하나 있는데, 모델을 학습하는 데에 시간이 무지무지 많이 걸린다는 점이다. total itemset $I$가 커질수록, $\frac{\partial}{\partial x_u}$을 계산하기가 힘들어진다. 이는, $\sum_i$ Term이 모든 아이템에 대해 iteration을 요구하기 때문이다. 이를 해결하기 위해, 논문의 저자는 Itemset $I$의 아이템중 일부만 샘플링 한 뒤 트레이닝하는 방법을 제안했다.

Approximating full loss using negative sampling

Gradient를 Approximate하는 방법에 대해 제대로 설명이 안 되어 있어서 유도해봤다. 논문에서도 언급되어 있듯 모델이 그리 어렵지 않아 근사식을 유도하는 것도 어렵지는 않았다.

위에서 정의된 Loss 함수는 일부 negative item을 선택하기 위해 딱 맞춰져 있는 것 같다. 이를 위해 Beta distribution을 사건의 확률로 가정한게 아닌가 싶다. Negative item만을 sampling하기 위해 $\frac{\partial}{\partial x_u}$을 풀어 써 보면 다음과 같다.

$I^+$은 유저의 interaction이 존재하는 아이템들, $I$는 전체 아이템셋을 말한다. 편의상 regularization은 생략했다.

저기서 오른쪽 항의 마지막 텀인, $\sum_{i\in I} \frac{\exp(r_{ui})}{1 + \exp(r_{ui})}y_i$을 보면, $i \in I$에서 하는 부분을 $\vert I’ \vert « \vert I \vert$가 성립하는 $I’$에 대해서 sampling해도 괜찮을 것 같지 않은가?

식을 간단히 바꿔 적어 보자.

마지막 텀을 전체 아이템을 iterate하지 않고, 아이템의 서브셋에서 iterate하는 것으로 model의 time complexity를 다음과 같이 줄일 수 있다.

$k$는 유저와 아이템의 평균적인 interation 횟수이다.

또한, $I’$을 만들 때 positive item을 포함하는 이유는, 각 유저 별로 Negative item을 detect해서, 이 안에서 샘플링을 하는 것이 엄청 inefficient하기 때문에, 이를 보상하기 위해 두번째 텀에 $(1+c_{ui})$ 대신 $(c_{ui})$를 곱해주었다.

만약 positive item이 sampling되었을 경우

가 되어 원래 gradient 식의 두번째 항이 된다.

Loss approximation을 했을 때의 성능 그래프

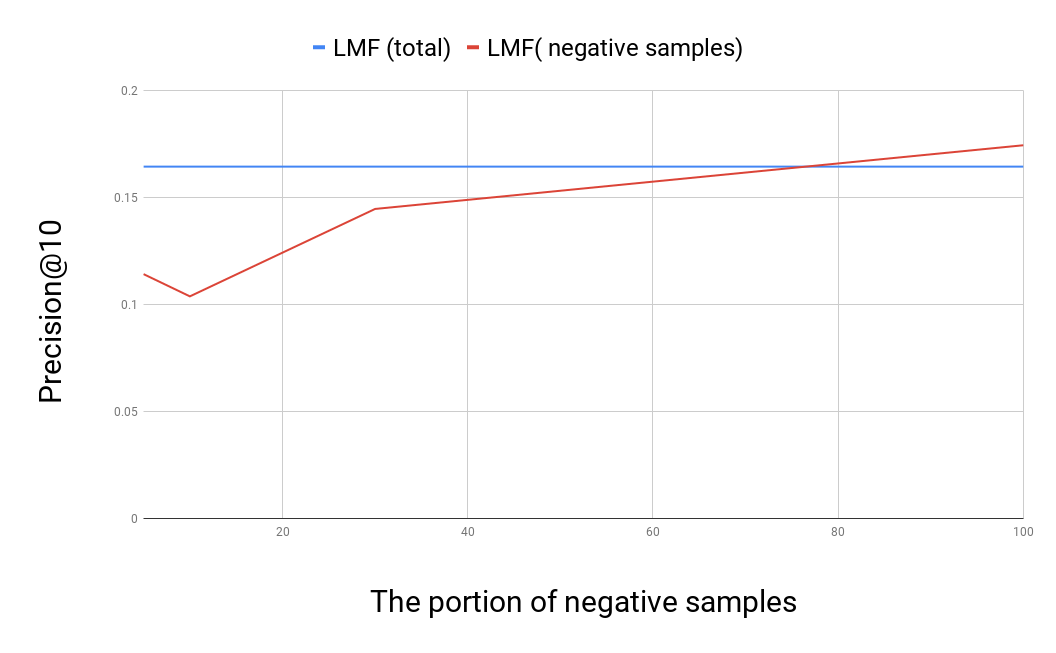loss를 approximate하기 위해 사용하는 sample의 비율(positive interaction의 K배 많게 하는 K)를 조정해가면서, Movielens 100k 데이터셋에 대해 트레이닝한 결과이다. K가 적당히 클 때, 전체 데이터를 사용하는 것 만큼이나 효율적임을 알 수 있다.implementation이 그리 efficient하게 되지는 않아서… 속도에 대한 비교는 할 수 없는게 아쉽다.

이를 파이썬으로 구현하면 다음과 같다.

    def get_deriv(self, idx, user=True, portion_neg_samples=10):
        if user:
            mat = self.Cui
            user_vectors = self.user_vectors
            item_vectors = self.item_vectors
            num_items = self.num_items
        else:
            mat = self.Ciu
            user_vectors = self.item_vectors
            item_vectors = self.user_vectors
            num_items = self.num_users

        pos_item_indices = mat.indices[mat.indptr[idx]:mat.indptr[idx + 1]]
        pos_confidences = mat.data[mat.indptr[idx]:mat.indptr[idx + 1]]
        num_pos_interactions = len(pos_confidences)

        #일부 아이템만을 샘플링해서 이용하고 싶은 경우
        neg_item_indices = np.random.choice(num_items, min(num_pos_interactions * portion_neg_samples, num_items))

        # 전체 아이템을 이용하고 싶은 경우
        #neg_item_indices = np.arange(num_items)
        pos_item_vectors = item_vectors[pos_item_indices]
        neg_item_vectors = item_vectors[neg_item_indices]

        A = np.dot(pos_confidences, pos_item_vectors)

        ret = self.u_score(user_vectors, item_vectors, idx, pos_item_indices)
        ret = (pos_confidences * ret) / (1 + ret)
        B = np.dot(pos_item_vectors.T, ret)

        ret = self.u_score(user_vectors, item_vectors, idx, neg_item_indices)
        ret = ret / (1 + ret)
        C = np.dot(neg_item_vectors.T, ret)
        _uv = user_vectors[idx].copy()
        _uv[-2:] = 0.
        deriv = A - (B+C) - self.reg_param * user_vectors[idx]

성능 비교

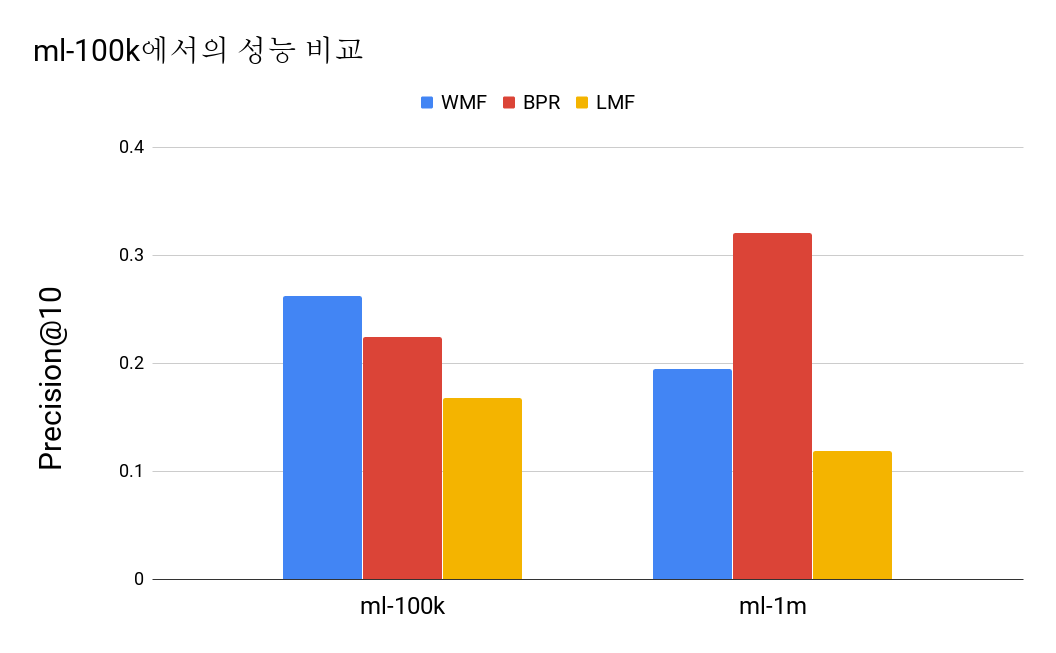
모델이 그리 성능이 좋지 않은 것 같다… MovieLens dataset에서만 그런 걸 수도 있겠는데, 이런 정도라면 추천하는데 사용하긴 힘들 것 같다.

다만, 유저 $u$가 특정 아이템 $i$를 좋아할 확률을 모델링 할 수 있다는 점에서,

이런 걸 구현하는 데에 응용하면 좋지 않을까 생각한다.

결론

논문을 읽으면서 엄청 Clever한 아이디어이고, 대단하다고 생각을 했는데, 이를 실제로 (간단하게지만) 구현해보면서 조금 실망했다.

우선 이 모델은 (1)Hyperparameter에 굉장히 민감하고, (2) Adagrad같은 방법을 써서 Gradient step의 크기를 굉장히 작게 하지 않으면 모델을 트레이닝 할 수 없다. 마지막으로, (3) Relevence 관련 성능이 굉장히 좋지 않다. 내가 모델 튜닝을 대충 해서야

그렇지만, user와 item의 implicit interaction을 확률적으로 묘사하려는 (내가 알기론) 최초의 시도이며, 이를 성공적으로 해냈다는 점이 대단한 점인 것 같다.

References:

[1] Logistic Matrix Factorization for Implicit Feedback Data, https://web.stanford.edu/~rezab/nips2014workshop/submits/logmat.pdf