[WIP]

Neural Combinatorial Optimization with Reinforcement Learning

잡담

1. 회사에서 맥을 받았다. 오예… 맥으로 쓰는 첫 블로그 포스트. 익숙해지질 않는다 ‘ㅅ’… 벌써 한달이나 됬는데, 코드도 제대로 못 짜겠고, 블로그에 글도 제대로 못 쓰고 있다. 근데 맥 생각보다 이쁘자너…불편하지만…이쁜것… 그것이 갬성..

2. 요즘 집중을 잘 못하겠다. 우울한 기분은 조금 나아진 것 같은데, 왜 우울함이 끝나면 산만함이 찾아오는 걸까. 나는 공부를 할 수 없는 운명인 것일까… 그런 것일까… 그런 것이다..

3. 포스트를 간단하게 쓰기로 결심했다. 어차피, 논문을 직접 읽는 일을 대체할 수는 없다고 생각하고… 그냥 이게 무슨 일을 하는 거다…라는 내용을 비교적 짧은 시간에 전달할 수 있으면 좋은게 좋은거 아닐까 하는 생각이 들었다.

Nearest Neighbor search in Recommender System

추천 시스템에서 많은 가장 많이 하는 일 중 하나는 특정 아이템와 유사한 아이템를 찾는 일이다. 이는 주로 다음과 같은 방법을 통해 이루어진다.

1. 아이템들을 어떤 벡터 공간에 임베딩한다.
2. 아이템의 유사도를 측정할 기준을 정한다.
3. 정한 유사도를 바탕으로, 유사한 아이템을 선택한다.

(1)은 주로 Collaborative filtering을 이용해서 만든다. (2)는 주로 cosine similarity를 이용한다. (3)은 $cos(i_q, i_1), cos(i_q, i_2), …, cos(i_q, i_M)$을 다 계산한 뒤에, 이 중 가장 값이 큰 $k$개의 아이템을 선택해 돌려주면 된다.

(1), (2)는 단순히 생각하면 어려울 게 없다. (3)도 마찬가지다. 하지만, 하지만… 추천 시스템에서 다루는 데이터의 규모가 커지면 가장 먼저 문제가 생기는 곳은 (3)이다.

전체 아이템의 개수가 천만개인 경우를 생각해 보자. 한 아이템과 비슷한 아이템을 찾기 위해서는, $cos()$ 함수를 천만 번 호출해야 한다. 이는 당연히도 실시간으로 계산할 수 없다. 그럼, 미리 계산해 두는 것은 어떨까? 모든 아이템에 대해, 모든 아이템의 유사한 아이템을 계산하는 경우 천만*(천만-1) / 2의 공간이 필요하다. 이도 역시 불가능하다.

즉, 실시간으로 어떤 아이템과 유사한 k개의 아이템을 계산하기 위해서는, 단순히 모든 아이템과의 유사도를 계산해보는 것보다 나은 방법이 필요하다.

굳이 완벽하게 정확한 해(가장 유사도가 높은 k개의 아이템)을 구하지 않아도 괜찮으니, 더 빠르게 비슷한 아이템을 찾고자 하는 방법을 연구하는 분야가 approximate nearest neighbor search라고 하는 분야이다.

Navigable Small World Graph

문제 정의

\(\text{dist}(q, x) = (q - x)^2\)

일 때,

쿼리 아이템 $q$가 있을 때, $\text{dist}(q, x)$가 충분히 작은 k개의 아이템 $x_1, x_2, …x_k$을 리턴하기. 가장 작은이 아니라, 충분히 작은인 것에 유의하자.

Navigable Small world graph는 노드 간의 거리가 (가장 가까워지는 노드로 greedy하게 이동했을 때)평균적으로 $log(N)$($N$은 전체 노드의 수)에 가까운 그래프를 말한다.

알고리즘을 요약해 설명하자면 다음과 같다. (Graph를 구성되어 있다고 가정)

1. query q와 거리가 가까운 노드로 (빨리) 이동한다.
2. 그 노드 근처에 있는 노드들을 열심히 탐색해서 가까운 아이템을 찾는다.

즉, 이 알고리즘에서 중요한 포인트는, (1) 빠르게(node traversal count를 적게 하며) 쿼리 q와 거리가 가까운 노드로 이동해야 하며, (2) 어떤 노드의 이웃들은 그 노드와 가장 가까운 노드여야 한다. 이런 형태로 그래프를 구성할 수만 있다면, 우리는 쿼리 q와 비슷한(거리가 작은) 노드를 빠르게 찾아 리턴할 수 있을 것이다.

빠르게 q와 가까운 노드로 이동하기.

HNSW는 여러 개의 그래프를 만드는 것으로 (1) 빠르게 쿼리 q와 가까운 노드로 이동하는 어려움을 해결했다. 계층적 그래프를 다음과 같이 구성되어 있다고 하자.

이 그래프는 다음과 같은 특징을 갖고 있다.

1. node의 최대 degree가 M보다 작아야 한다.(layer마다 M은 다를 수 있음)
2. 위 레이어에 존재하는 노드는 반드시 아래 레이어에도 존재해야 한다.
   • 즉, layer 3에 존재하는 node는 layer 2, 1, 0에도 존재해야 한다.

layer 2(높은 레이어)는 정확한 용어는 아니지만, sparse하고, 낮은 레이어로 갈 수록 인접한 노드 간의 거리가 짧아지고, 노드가 많아지는 것을 확인할 수 있을 것이다.

높은 레이어는 node가 적고, 인접한 노드 사이의 거리가 길다. 즉, 적은 hop 수로 많은 거리를 이동할 수 있으며, 한번 이동시마다 쿼리 q에 많이 가까워진다고 생각할 수 있다. 더 이상 가까워질 수가 없으면 아랫 레이어로 이동해서, 탐색한다. 아랫 레이어에는 윗 레이어보다 노드의 수가 더 많지만, 노드 간의 거리가 더 짧아진다.

Toros N2 발표에서 들은 아주 좋은 비유가 있었는데,

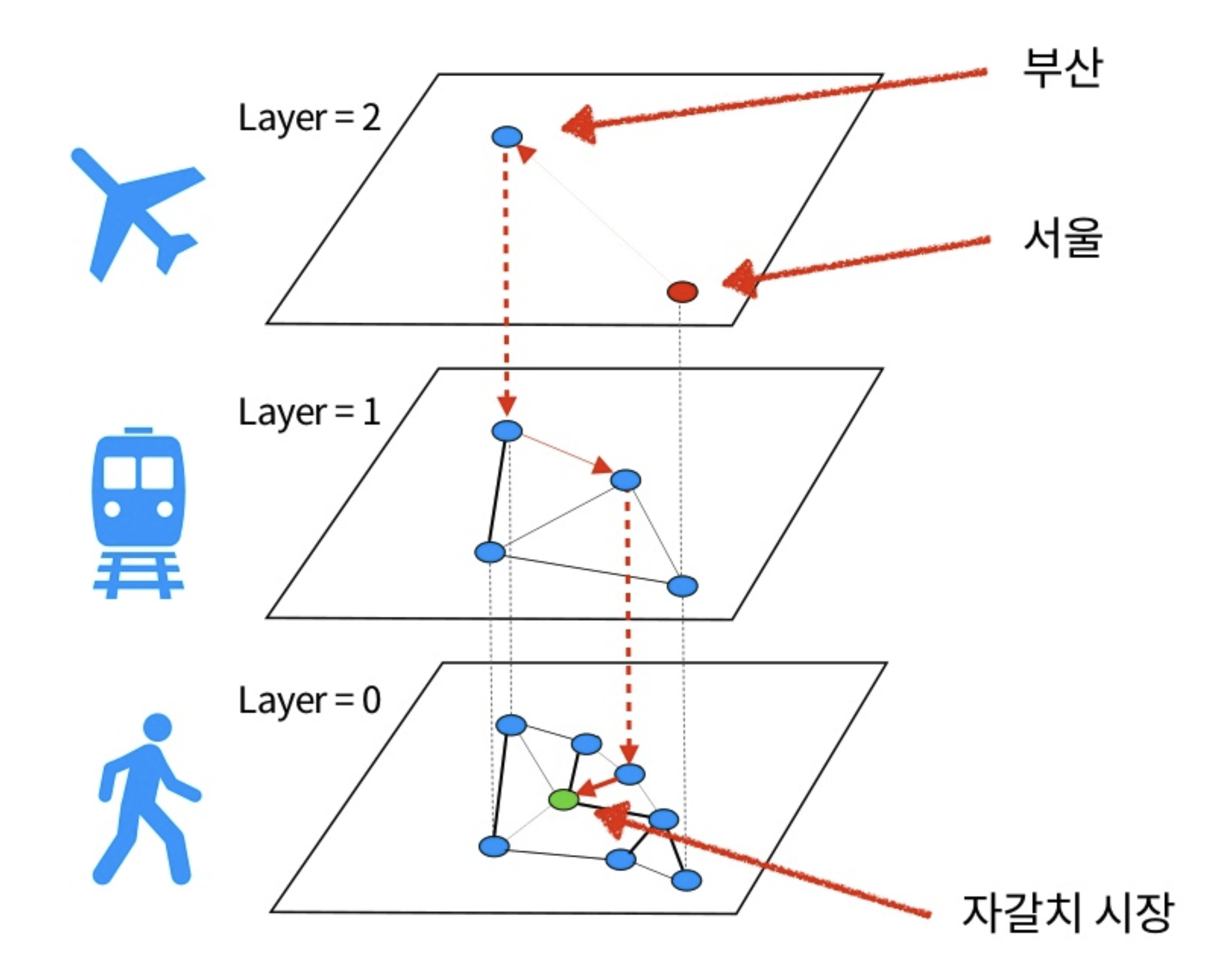
수원에 사는 내가, 자갈치시장 가려면 다음과 같은 루트를 밟아야 한다. 직선거리로는 나빠지지만, 결국 더 빠르게 갈 수 있는 서울역에 간다. 그 다음 부산역으로 가야 하는데, 가는 도중에 자갈치시장을 지나쳤을 것이다(다만 아주 빠르게) 그 다음엔 지하철을 타고, 자갈치시장으로 이동하는데, 역시 내가 가려는 목적지에 (정확히는 아니지만) 가까워지고 있다. 마지막으로, 가장 세밀하게 걸어서 목적지에 도착할 수 있을 것이다. 이 과정을 수도코드로 적자면 다음과 같다.

    node e = random node at layer l
    while l>= 0:
        while True:
            if 노드 e의 layer l에서의 이웃 중 q와의 거리가 더 짧은 것이 존재:
                e를 그 이웃으로 업데이트
        l -= 1
    return e

도착한 q와 가까운 노드 e에서, 비슷한 노드들을 K개 찾기.

q와의 거리를 기준으로 한 priority queue를 만들어서, BFS를 수행한다.

BFS의 중단 조건은 다음과 같다. K개의 node를 모두 찾았는데, 그 k개의 node의 이웃 중 $\text{dist}(q, n) < \text{dist}(q, e)$, where $n \in {Neighbors}(W)$ and $e \in W$ where $W$는 지금까지 찾은 노드의 집합, $\text{Neighbors}(W)$은 $W$ 내의 모든 node들의 이웃의 집합이다.

(저런 계층적 그래프가 잘 만들어져 있다고 하면) 그래프 안에서 쿼리 q와 가까운 노드를 찾을 수 있다.

계층적 그래프 만들기.

이제 계층적 그래프 만드는 방법에 대해 알아보자.

목표는 새 element $q$를 그래프에 삽입하기이다.

새 element $q$의 layer $l$을 랜덤하게 선택한다. $l$ ~ $-log(uniform(0, 1)) * m_L$을 따르게 선택하며, $m_L$은 hyperparameter이다.

이 되게, l을 draw한다. 새롭게 뽑은 Layer $l$은 기존 그래프의 최대 레이어 $L$보다 클 수도 있고, 작을 수도 있다.

element $q$는 layer $l$, $l - 1$, … $0$에 존재해야 하고, 이 층에서 neighbors를 갖는다.

삽입을 하기 위해, graph를 traverse해야 하는데, 그 시작 포인트인 enter point(layer L에 존재)를 임의로 정해 준다. (결정하는 방법은, 논문 참고)

이를 만족하는 $l$, $L$, $q$, $ep$가 존재한다면, 삽입을 진행할 수 있는데, 알고리즘은 다음과 같다.

    for lc in min(L, l), ... 0:
        W = q layer lc에서 q와 가장 가까운 C개의 elements
        for node in W:
            connect(q, node)
            if num_neighbors(node) > M
                node와 거리가 가장 먼 neighbour를 제거한다.
    ep = q

가장 중요한 포인트는, 개별 노드의 neighbors 수를 M개 이하가 되게 조절해주는 부분이다. 이래야 search가 빨라진다고 하는데, 자세히는 잘 모르겠다.

결론

간단하게 적는다고 적었는데, 간단하기는 커녕, 중요한 부분은 빠트리고, 중요하지 않은 부분만 자세히 적지 않았나 하는 생각이 든다. 근데, 하지만, 음… 정말 자세히 이해하고 싶은 사람은 논문을 보는게 맞는 것 같고 나는 음 내가 이 논문을 읽었고, 이해했다는 것과, 이 글을 읽은 사람이 논문의 대략적인 개요를 이해하고, 관심이 더 있으면 논문을 직접 읽어보게 하는게 중요하지 않을까 하는 생각이 든다.

References

Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs

카카오 n2 발표 (2018년도 if kakao)