TSP 문제를 강화 학습으로 풀기

Neural Combinatorial Optimization with Reinforcement Learning

Attention, Learn to Solve Routing Problems! 논문 리뷰입니다. 설명은 됬고, 코드를 보고 싶어 하실 분도 계실 것 같습니다 ‘ㅅ’… 논문에서 리뷰한 Attention, Learn to Solve Routing Problems!과 Neural Combinatorial Optimization with Reinforcement Learning 논문을 함께 구현해 깃헙 링크에 올려두었습니다.

잡담

의외로 많은 문제들이, 복잡한 강화학습 기술을 사용하지 않고, 단지 두 가지 테크닉을 (엄청 잘 했지만) 이용해 새로운 도메인에서의 문제를 멋지게 해결해내는 경구가 많습니다. 두가지 테크닉은 다음과 같아요.

1. Neural Network을 이용한 Function Approximator를 만든다.
2. Policy Gradient(REINFORCE Algorithm)만으로 대단한 일을 하는 경우가 많습니다.

저도 이런 논문을 열심히 읽어서, 기계 학습을 일견 전혀 상관없어 보이는 분야에 적용해 멋진 일을 하고 싶습니다.

Traveling Salesperson Problem

Traveling Salesperson Problem은 조합론, 컴퓨터 과학에서 굉장히 널리 알려진 문제이다. 점들의 집합이 주어져 있을 때, 모든 점을 순회하고 자기자신으로 돌아오는 경로 $\pi$ 중 길이가 짧은 $\pi$를 찾는 문제이다. 조금 더 자세한 정의는 TSP 위키피디아 설명를 참고하면 좋을 것 같다.

이 문제는 어려운 걸로 유명하다! 정확한 해를 구하는 것은 다항시간 내에 불가능하다는 것이 이미 알려져 있고, 그래서 충분히 좋은 근사치를 계산하는 알고리즘이 많이 나와 있다. 이 논문도, 그런 근사치를 구하는 알고리즘 + 1일 뿐인데…. 다만, 다른 점은, 강화 학습을 이용하는 풀이를 제안했다는 점이다! 이게 얼마나 대단한 일이냐면, 강화 학습을 이용한 방법은, 문제에 대한 사전지식이 사실상 없다는 점이다! 즉, 다른 복잡하거나 어려워서, 휴리스틱을 제안하기 힘든 문제에 대해서도 강화학습이 충분히 좋은 Solution을 줄 수 있다는 점을 보였다는 점이 이 논문의 큰 Contribution이라 생각한다.

제안 방법

개별 점들을 Attention Mechanism을 이용해 개별 점들을 Encode하고, 이를 이용해 point들의 집합 전체를표현하는 방법을 제안합니다. 제안된 방법은 Transformer와 상당히 유사합니다. Transformaer 모델에 대해 추가적으로 관심이 있으신 분들은 좋은 포스트를 참고하면 좋을 것 같아요.

Encoder

Encoder는 세 가지 단계로 이루어져 있다.

1. Point Embedding
2. Multi-head self attention layer

전체적인 구조는 (정말 대충 그렸지만) 다음과 같다.

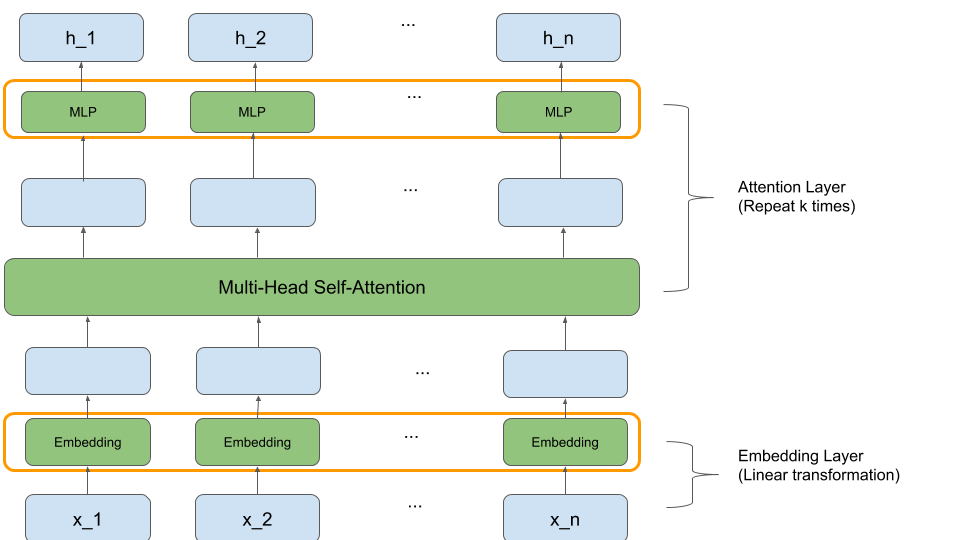
Point Embedding

각각의 point는 TSP 문제의 경우 2차원이다. 이 2차원 벡터를 $d_h$차원 스페이스로 embedding하는데, 이는 간단한 affine projection으로 표현할 수 있다.

\[h_i^{(0)} = W^x x_i + b_x\]

Multi-head self attention layer

개별 point를 다른 point와의 관계를 함께 포함시킨 표현으로 임베딩하기 위해, 저자는 self attention을 제안했다.

$H = [h_0^{(0)}, h_1^{(0)}, \cdots, h_n^{(0)}]$ 을 skip-connection이 있는 Attention layer(Multi-head Self-attention과 Positionwise feed-forward network)에 넣어 준다.

\[H^{(l+1)} = H^{(l)} + \text{SelfAttention}(H^{(l)})\]

추가적으로, 개별 레이어마다 Batch normalization을 추가해준다.

이 결과를, Transformer의 방법과 같이, 다시 한번 Attention layer에 넣어주고, 하는 repeat를 몇 차례 반복하면 개별 points의 embedding이 완성된다. 논문에서는 Attention layer를 세차례 거치는 것이 성능과 계산 속도 측면에서 둘 다 적절하다고 적어놓았다.

이렇게 결과적으로 생성한 points $p_1, p_2, … p_n$의 임베딩들을 \(H = [h_1, h_2, \cdots, h_n]\) 이라 하자. 또한, 이 집합 전체의 표현을 \(\bar h = \frac{1}{n} \sum_i h_i\) 이라 하자.

이 두 값을 이용해, 다음에 어떤 point를 선택할 지를 결정하는 것이 Decoder이다.

Decoder

디코더는 $n$번의 step으로 이루어져 있다. 한 스텝마다, 하나의 point를 리턴한다. 즉, 디코더는 point set ${p_1, p_2, …, p_n}$에 대한 permutation $\pi$를 생성하는데, 이게 TSP의 traverse order와 동일하다.

Attention(Pointer)에 사용할 입력으로, timestep마다 다른 $p$를 만들어 사용한다. 사용하는 정보는 다음과 같다. (1) 그래프 임베딩 정보, (2) 가장 마지막에 방문한 point의 임베딩, (3) 가장 처음에 방문했던 point의 임베딩이다.

\(p = \begin{cases} \text{concat}(\bar h, h_{\pi_1}, h_{\pi_{t-1}}) & t > 1 \\ \text{concat}(\bar h, e_1, e_f) & t = 1 \end{cases}\) 이전에 방문한 point가 있는 경우, (첫번째 선택이 아닌 경우) 가장 처음 방문했던 point와, 가장 마지막에 방문했던 point를 Context로 묶어 준다. 이전에 방문한 point가 없는 경우, learnable embedding $e_1, e_f$를 placeholder로 그냥 넣어 준다.

Glimpse

Pointer(이후 설명)에 query로 사용되는 $p$를 조금 더 잘 표현하기 위해, 구체적으로는 아직 선택되지 않은 points에 조금 더 relevant하게 만들기 위해 $p$에 다시 한번 masked attention을 통과시켜 준다.

\[p' = MHA(p, [h_1^{(F)}, \cdots, h_n^{(F)}])\]

$p$를 조금 더 잘 표현하기 위해, 이를 다시 한 번 어텐션을 거치도록 만들어 준다. 이미 방문했던 point는 Attention score를 계산할 때 제외하는 Attention을 다시 한 번 적용해 준다. 이는 다음과 같이 처리한다.

\[l_j = \begin{cases} \frac{q^Tk_i}{\sqrt{d_k}} & \text{if }j \neq \pi_{t'} \forall t' < t\\ -\infty & \text{otherwise} \end{cases}\]

Pointer

Pointer Networks 논문에서 제안된, 어텐션의 Variant이다.

위에서, $Attention(p, H)$를 계산할 때 $[0, 1]$ 사이의 weight vector $\alpha$가 계산된다. 이 Alpha를 확률 분포로 해석하는 것으로, Attention은 $n$개의 입력 중 하나를 선택하는 확률 분포를 만드는 모듈로 생각할 수 있다.

다만, logit을 계산하는 부분이 조금 다르다.

\[l_j = \begin{cases} C \tanh\frac{q^Tk_i}{\sqrt{d_k}} & \text{if }j \neq \pi_{t'} \forall t' < t\\ -\infty & \text{otherwise} \end{cases}\]

$\tanh$ 함수와 $C$를 이용해서, logit이 너무 커지거나, 너무 작아지는 것을 막는다. 이는 Pointer Networks 논문에서 (아마) 처음 제안된 것이다.

그럼, 위에서 계산한 logit $l_j$를 이용해, point $i$를 선택할 확률을 계산할 수 있다. \(p_{\theta}(\pi_t = i \vert s, \pi_{1:t-1})= p_i = \alpha_j = \frac{\exp(l_j)}{\sum_{j'} \exp(l_{j'})}\) 이 확률 벡터를 계산했으면 Policy Gradient를 통해 이를 계산할 수 있다.

다만, $\alpha_i$를 계산할 때, 위에서와 마찬가지로 이미 방문했던 point는 방문해야 하지 말아야 한다.

설명하지 않은(사실 못한) 것들…

사실 Combinatorial optimization을 다른 분야에 적용해보기 위해서 논문을 읽고 구현해보다가, 조금 더 자세히 기록해두고 싶어서, 중요한 포인트를 집어서 적었는데, 사실 논문에는 더 많은 내용이 있다. 관심이 가는 분들은 논문을 직접 읽어보면 정말 좋을 것 같다. 사실, 내 글을 읽고 원 논문에 관심이 생긴다면 기쁠 것 같다.

• TSP 문제가 아닌, 다른 여러 조합론 문제도 제안된 모델을 통해 해결할 수 있음을 보임
• 새로운 Greedy Rollout 방법을 제안함

구현체

논문에서 리뷰한 Attention, Learn to Solve Routing Problems!과 Neural Combinatorial Optimization with Reinforcement Learning 논문을 함께 구현해 깃헙 링크에 올려두었습니다.