들어가며
- Note: 기본적으로, 패턴 인식은 여러 분야에서 발전했다기보다.. 저도 이곳저곳 주워들어가며 공부해서 이론적인 지식을 사혼의 구슬 모으듯 조금조금 모았기 때문에, 개인적으로 사혼의 구슬 조각 여러 개가 모인 게 아니라, 하나의 지식 덩어리로 이해하고 싶어서 정리하는 내용이기도 합니다. 틀린 부분이 많고 딱히 검증되거나 proofreading을 받은 적도 없습니다. 따라서, 누군가가 읽고 지적해주면 짱 좋을 것 같습니당.
머신 러닝이 뭘 하는 걸까?
이 장에서의 예시는, $\mathcal{X} = $ (키, 몸무게) 공간, $\mathcal{Y}=$ 생물학적 성별 = {남성, 여성}이라고 생각하면 좋다. $x$, $y$는 각각 $\mathcal{X}$, $\mathcal{Y}$의 한 원소를 말한다.
Let define a concept $\mathcal{C}$ a family of measurable functions
\[\mathcal{C}: \mathcal{X} \rightarrow p(\mathcal{Y} \vert \mathcal{X})\]Conept는 여러 가지일 수 있지만, “한 가지 문제”라고 생각하면 좋다. 예를 들어서, 국가별로 Concept $\mathcal{C}$가 다를 수 있다. 한국에서 $x= (168cm, 62kg)$라면, $y$는 남성일 확률이 비교적 높겠지만, 네덜란드에서는 같은 $x$라고 해도, $P(y=\text{여성} \vert x)$이 더 높을 것이다.
그리고, hypothesis $\mathcal{H}$을 정의하자.
\(\mathcal{H}: \mathcal{X} \rightarrow y\) where somehow we can choose $h \in \mathcal{H}$. 이를테면, $h = (w, b)$이고 , $h = \mathbb{I}[w^Tx+b > 100]$인 경우를 생각할 수 있다. 우리는 적당한 방법으로 $h$, 즉 $w, b$를 선택할 수 있어야 한다. 이 과정은 머신러닝에서는 fitting이라던가, learning이라던가, finding posterior라던가, burn-in이라던가, 암튼 여러 이름으로 부르는데, 아무튼..
이 글에서는.. 추가적으로 $\mathcal{H}$이 deterministic이라고 가정한다.실제로는 그렇지 않아도 괜찮을 뿐더러, 거의 모든 통계적 머신 러닝 방법은 $\mathcal{H}$가 확률 분포를 모델링한다.
Error
어떻게 가설 집합 $\mathcal{H}$을 만들었는지, 그 가설 집합 내에서 $h$를 어떻게 선택했는지는 일단 건너뛰고, 우리가 어떻게든 $\mathcal{H}$와 $h$를 구했다고 가정하고 만들어진 가설이 얼마나 좋은지 평가하는 방법을 생각해보자.
Risk, or Error $R$.
\[R(h) = \mathop{\mathbb{E}}_{x'\in \mathcal{X}} \mathop{\mathbb{E}}_{y' \in p[y \vert x']}\left[\mathbb{I}(h(x') \neq c(x'))\right]\]Empirical Error
Empirical Error는 ${(x_1, y_1), (x_2, y_2), \dots, (x_m, y_m)}$을 관측했을 때의 저 값이라고 생각할 수 있다.
\[\hat{R}(h) = \frac{1}{m} \sum_{i=1}^m \left[\mathbb{I}(x_i \neq y_i))\right]\]$y_i$는 확률분포 $c(x_i)$의 한 sample입니다.
우리의 한계
위의 예제를 생각해 보면, 어떤 concept 내에서 알 수 있는 것의 한계가 존재한다.$x = (168cm, 60kg)$이 주어졌을 때 이 사람이 남자인지 여자인지 확실히 알 수는 없다. 머리카락의 평균 길이라던가, 유전자라던가…더 많은 정보가 주어진다면 얘기가 다르지만… 가설 $h$를 찾으려고 최선을 다했을 때 생기는 에러가, 우리의 한계이며, 이를 Bayes Error라 부른다.
\(R^* = \inf_{h \text{ is measurable}}(R(h))\)
is measurable에 크게 실용적인 의미는 없다. 혹은
파이토치로 구현될 수 있는뭐 이런 의미랑 같다.
Bayes Error가 만드는 가설 $h^*$를 정의할 수도 있다. \(h_{\text{Bayes}}(x) = \text{argmax}_{x} c(x) = \text{argmax}_{x}([p(y_1 \vert x), p(y_2 \vert x), ..., ])\)
우리가 제거할 수 없는 Error는 Noise라고 부르고 $\text{Noise} = 1 - \frac{1}{m}r(h^*(x))$으로 정의한다.
노이즈가 큰 문제는 본질적으로 풀 수 없다. 노이즈가 크다는 것은 보통 $x$와 $y$의 관계가 없는 경우라고 생각하는데, 사실 꼭 그런 것만은 아니다. $y = $지구의 반지름이 1cm보다 큰 경우. 라고 했을 때, $x$가 어떤 공간에 놓여 있던간에, $y$는 참이므로… 뭐… 반례를 위한 반례지만 이런 경우도 생각할 수 있다.
그래서 지금까지 왜 노이즈 얘기를 했냐면… 머신 러닝으로 어떤 문제를 푼다에 대한 얘기를 이제 할 수 있기 때문이다. 우리가 잘 하고 싶은 일은,
\(\mathcal{L} = \text{argmin}_h[R(h) - R^* \vert \mathcal{H}]\)인데, 이를 일반적으로 손실 함수, 혹은 오브젝티브라고 한다. $\mathcal{L}$의 바람직한 성질을 유지하면서 뭔가를 곱하거나 더해주거나 로그를 취하거나 지수를 취하거나 한 것도 다 손실 함수, 혹은 오브젝티브라고 부른다.
이는 또 다시 이렇게 분리가 가능한데,
\(R(h) - R^* = \left[R(h) - \inf_{h' \in \mathcal{H}}R(h') \right] + \left[\inf_{h' \in \mathcal{H}}R(h') - R^* \right]\) 오른쪽 식의 왼쪽 항은 Estimation Error를 표현하는 텀이다. 오른쪽 식의 오른쪽 항은 Approximation Error를 표현하는 텀이다.
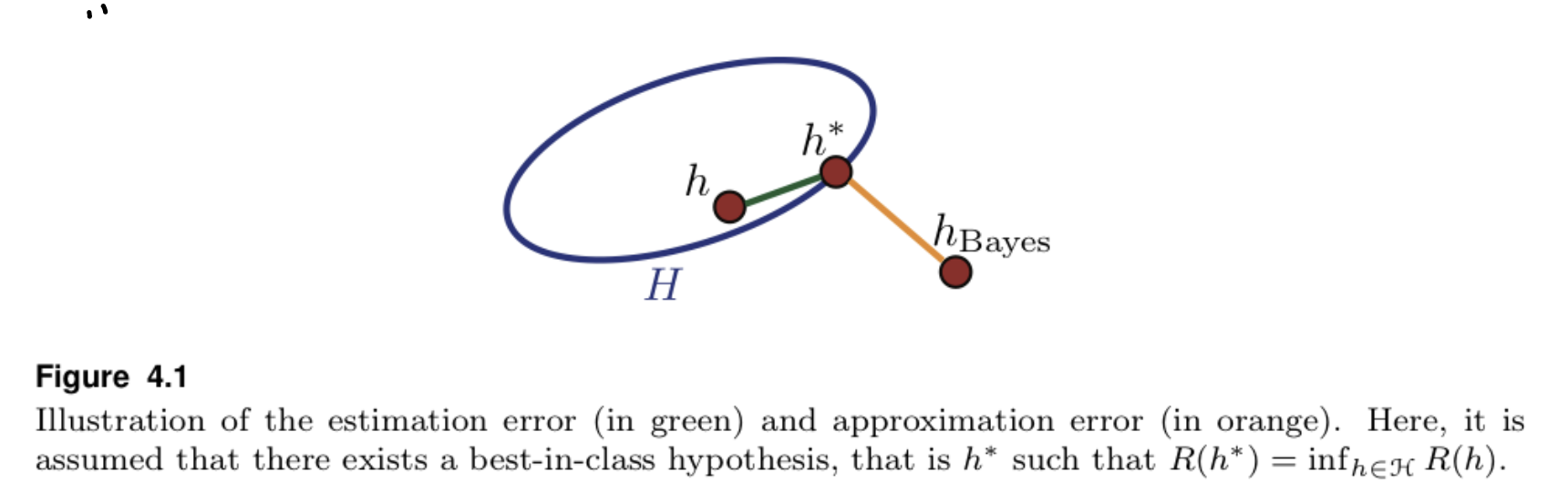그림으로 봤을 때.출처.
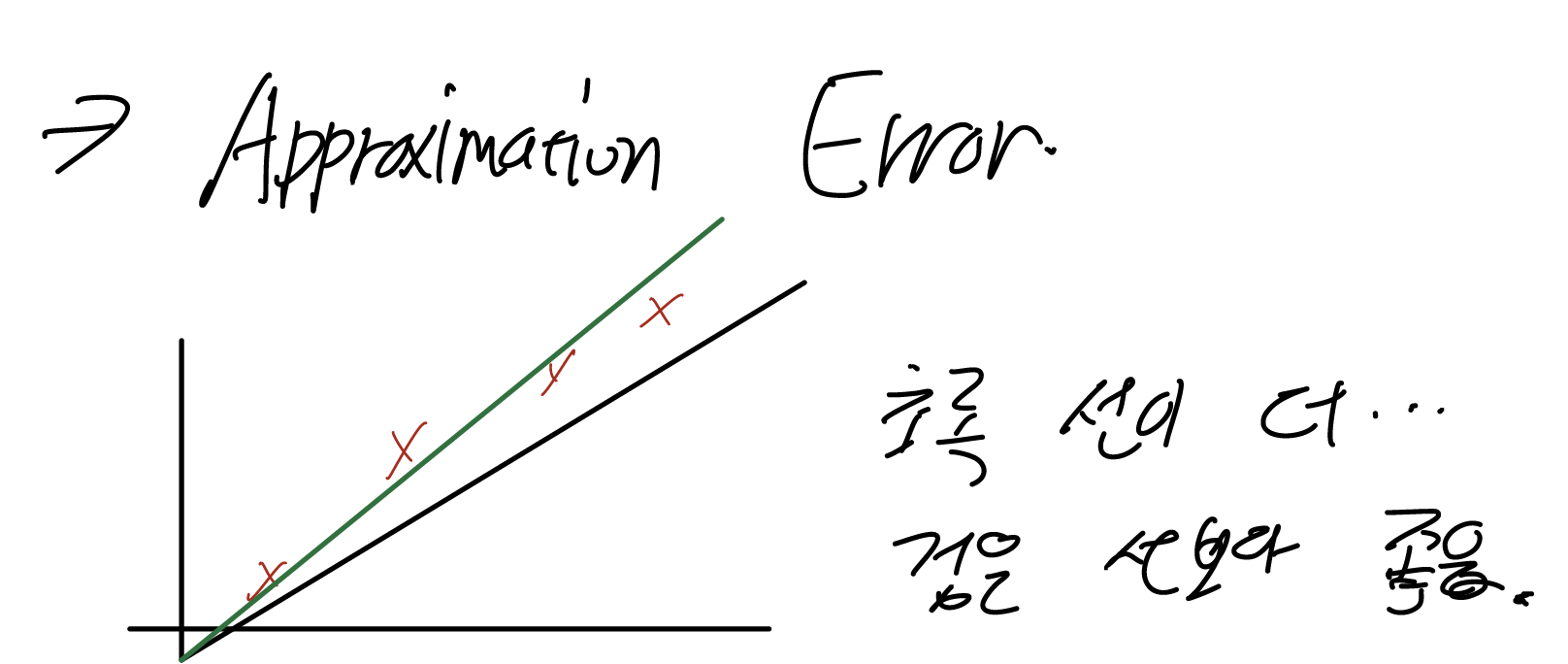Approximation Error의 예시. 같은 가설(0을 지나는 직선), Concept를 더 잘 설명하는 직선이 존재함.
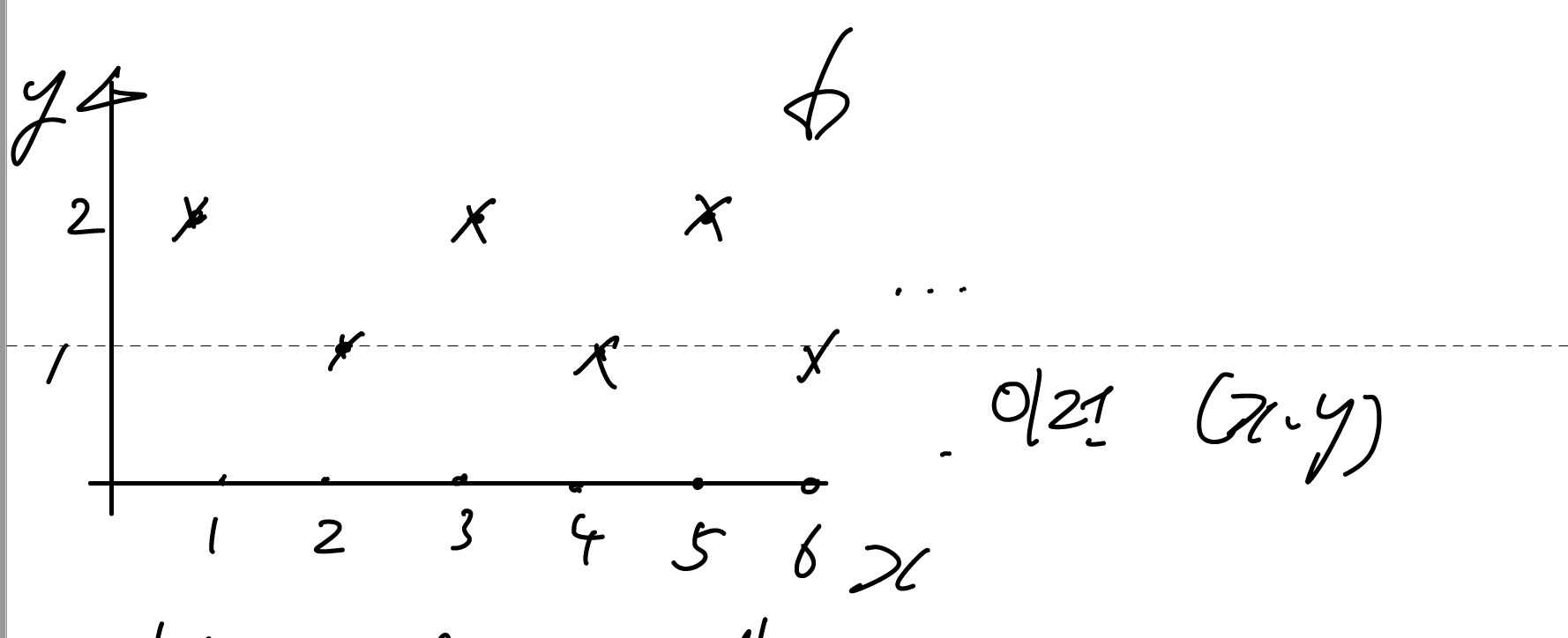Estimation Error의 예시. $y = 1 + x \text{ mod }2$의 경우 linear regression으로 오차를 충분히 잘 줄일 수 없음.
Estimation Error는 선택 공리 내에서의 최선과 내 현실 사이의 오차를 의미한다. “복잡한 딥러닝 모델을 학습할 때, Local Minima나 Saddle Point에 빠지지 않게 주의해야 한다”와 같은 얘기. Approximation Error는 내가 만든 가설의 한계를 의미한다. 예를 들면, “$y = cos(x)$를 근사할 때, x의 1차식으로 y를 근사하면 별로 정확하지 않다”와 같은 얘기.
머신 러닝 작업을 3개로 쪼개 본다면…
머신러닝을 분류할 때 흔히 사용하는 3가지 분류인, Supervised Learning, Unsupervised Learning, Reinforcement Learning을 이러한 관점에서 보았을 때 하나의 틀로 볼 수 있다. 그 경우 머신러닝 작업은 3가지의 (mutually exclusive하지 않은) 작업들로 쪼개볼 수 있다.
- 어떤 가설 집합 $H$를 사용할 것인지.
- Linear Regression, MLP, SVM, etc…
- hypothesis $h$와 concept $c$의 오차로 어떤 오차를 사용할 지.
- L2 Loss, Likelihood, KL divergence.
- Estimation Error를 어떻게 줄일 것인지.
- Least square, Gradient descen..
이 세 가지 작업은 연관이 꽤 크다. (3)에서 Least squares를 쓰기 위해서는 (1)의 해겵책은 Linear regression밖에 방법이 없고, (2)는 L2 loss를 가정하고 있다던가… 하지만 이론적으로는 3개는 어느 정도 독립적으로 연구가 되는 것 같다. 가설 집합에 관해서는 다음과 같은 학문 분야가 존재한다.
- MLP의 Universal Approximatior Theorem
- Nonlinear activation이 있는 hidden-layer가 1개 이상인 MLP는 데이터가 충분히 많다고 가정했을 떄, deterministic concept와의 오차를 원하는 만큼 줄일 수 있다. 2.. Rademacher Complexity: 가설 집합 $\mathcal{H}$의 복잡도가 어느 정도인지.
예시 1. Linear Regresion의 경우
(1) 어떠한 가설 집합을 사용할 것인지.
Least Squares $y = w^Tx$, where $w \in \mathbb{R}^d$.
Bayesian Linear Regression $y \sim \text{Normal}(y \vert w^Tx, \sigma^2)$
(2) 어떻게 오차를 표현할 것인지.
Let $y \sim \text{Normal}(y \vert w^Tx, \sigma^2)$. Then The likelihood $p(y_1, \dots, y_n)$ = $\prod_{i=1}^{m} \text{Normal}(y_i \vert w^Tx, \sigma^2) \propto$
\[(\sigma^2)^{-n/2} \exp\left[-\frac{1}{2\sigma^2} \sum_{i=1}^m (y-w^Tx)^2 \right]\]Take a log to the previous equation yields
\[-\frac{n}{2} \log( \sigma^2 ) + -\frac{1}{2\sigma^2} \sum_{i=1}^m (y-w^Tx)^2\]Let us treat $\sigma^2$ as a constant and just leave terms related to $w$ gives us
\(\text{Maximize } -\sum_{i=1}^m (y-w^Tx)^2\) or equivalently,
\[\text{Minimize } \sum_{i=1}^m (y-w^Tx)^2\](3) 오차를 어떻게 줄일 것인지.
우리가 고칠 수 있는 건 $w$ 뿐.
3-1 Gradient Descent
$w \leftarrow w - \lambda \frac{\partial}{\partial w}\sum_{i=1}^m (y-w^Tx)^2$
3-2 Least Ssquare
Let $w$ be a solution of the equation $\frac{\partial}{\partial w} \sum_{i=1}^m (y-w^Tx)^2 = 0$.