Translation of the post Embedding Sets of Vectors With EMDE
피쳐 엔지니어링으로서의 Vector Aggregation
EMDE는 인풋과 아웃풋만을 생각한다면, 벡터들을 하나의 고정된 길이의 벡터로 변환하는 연산이다. 여러 벡터를 하나의 단일 벡터로 표현하는 연산은 그다지 쓸모가 없을 것 같지만 실제로는 상당히 흔한 연산이다. 특히 추천 시스템에서, 한 유저의 표현을 유저가 소비한 아이템의 목록으로 표현하기로 했을 때…
모든 음식들에 대한 좋은 임베딩을 갖고 있다고 가정해보자. 다른 좋은 임베딩과 마찬가지로, 음식의 임베딩끼리 어떤 거리 관계가 성립할 것이다. 또한, 당신은 유저의 목록도 갖고 있어서, 그 유저가 어떤 음식들을 좋아하는지 알 수 있다고 생각해 보자. 우리의 목적은, 잘 표현된 음식들의 임베딩과, 유저들이 어떤 음식을 소비했는지를 통해 유저의 임베딩을 표현하는 것이다.
Aggregrating vectors as density estimation.
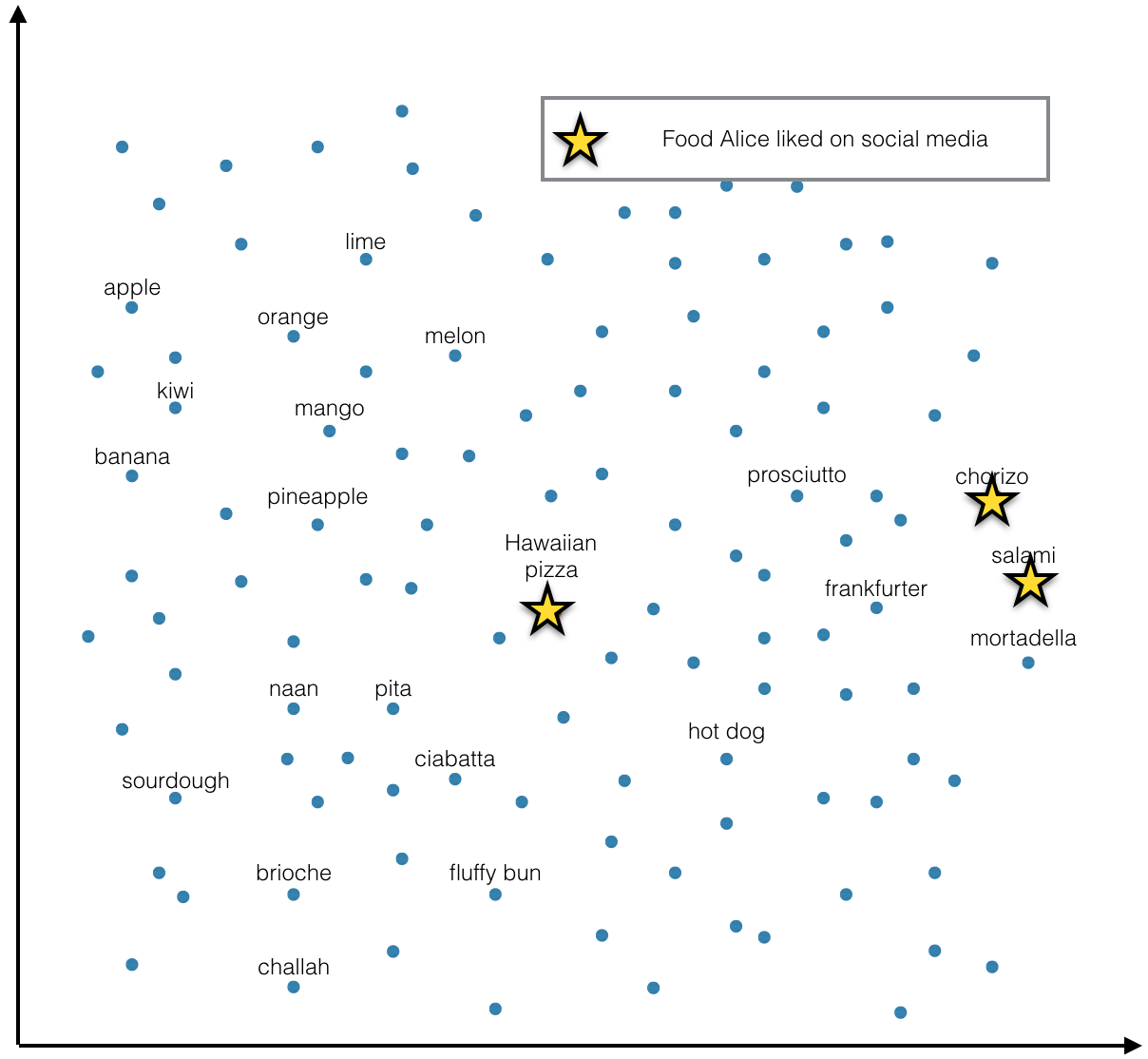
임베딩 공간에서, 어떤 유저가 좋아하는 아이템의 분포 (유저 선호도 분포)를 생각해볼 수 있다. 그리고, 유저가 실제로 클릭한 아이템은, 그 분포에서 가져 온 샘플이라고 생각할 수 있을 것이다. 유저가 클릭한 아이템을 샘플이라 생각해, 유저가 좋아하는 아이템 분포를 추정하는 방식으로, 유저 선호도 분포를 estimate할 수 있다.
EMDE는 이 선호도 분포의 parameters를 임베딩 표현으로 사용한다.
EMDE
입력은 다음과 같다.
- 모든 아이템의 임베딩
- (한 유저 A에 대한 임베딩을 만들 때) A가 소비한 아이템들의 리스트
임베딩을 생성할 때 조절할 수 있는 패러미터는 다음과 같다.
$K$: The number of hyperplanes
$N$: The number of indipendent estimiations;
Procedure:
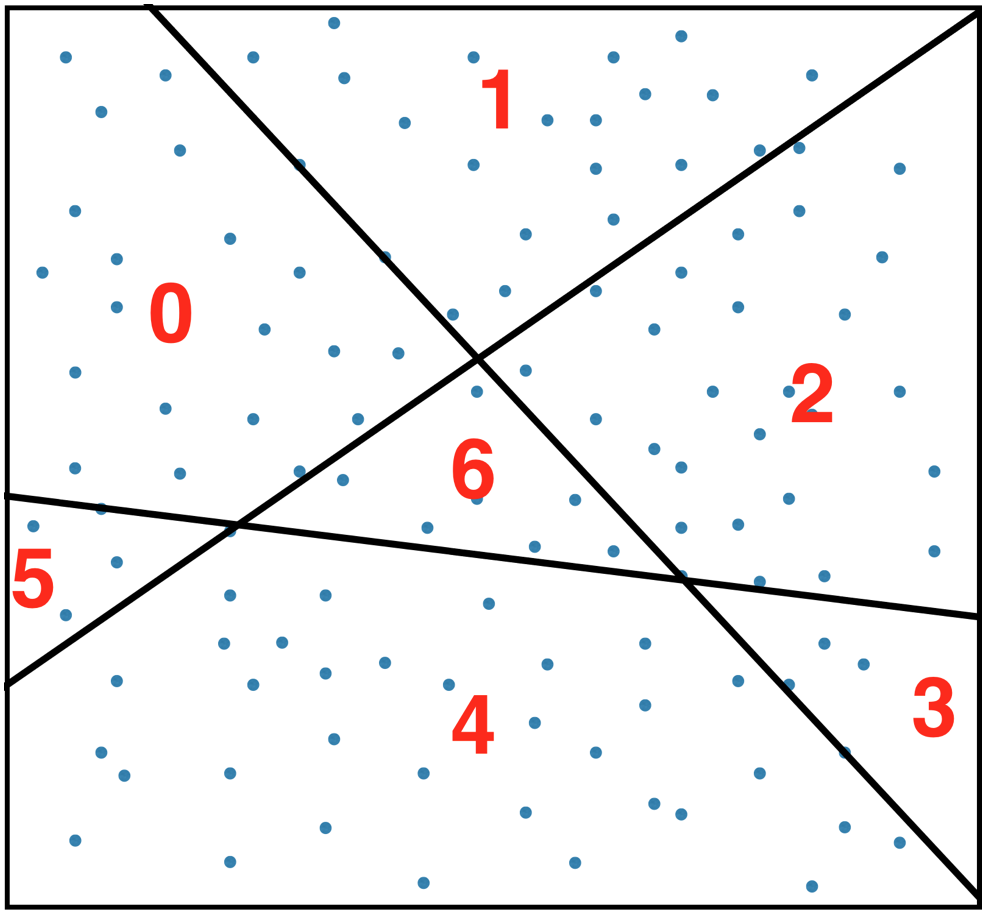
- 임베딩 공간을 다음과 같이 분할한다 $K$개의 선분으로 분할한다. 분할된 공간의 갯수는 최대 $2^{k}$개까지이다.
공간을 분할하는 선이 $l1, l2, l3$ 이렇게 있다고 해 보자. 임베딩 공간에서의 한 점 $p$는 $p^Tl1 + w_1$의 부호에 따라 선분이 어디 있는지 결정할 수 있는데(그 hyperplane의 위 혹은 아래), 모든 $k$개의 선분에 대해 이를 수행했을 때, 나오는 경우의 수는 $2^{k}$이다.
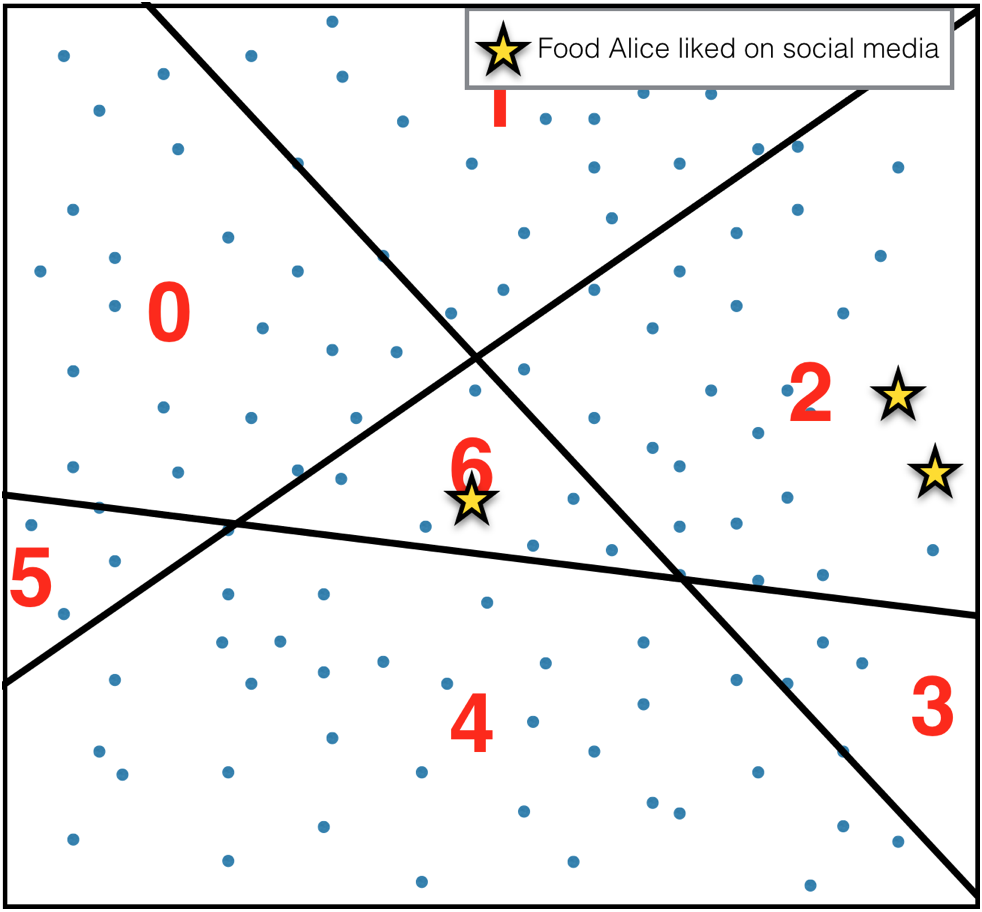
이 분할된 공간 속에, 유저가 소비한 아이템을 배치시키고, 이렇게 표현할 수 있다.
이 과정을 N번 반복하면, 비교적 정확한 유저 선호도 분포를 계산할 수 있을 것이다. (이런 식으로)
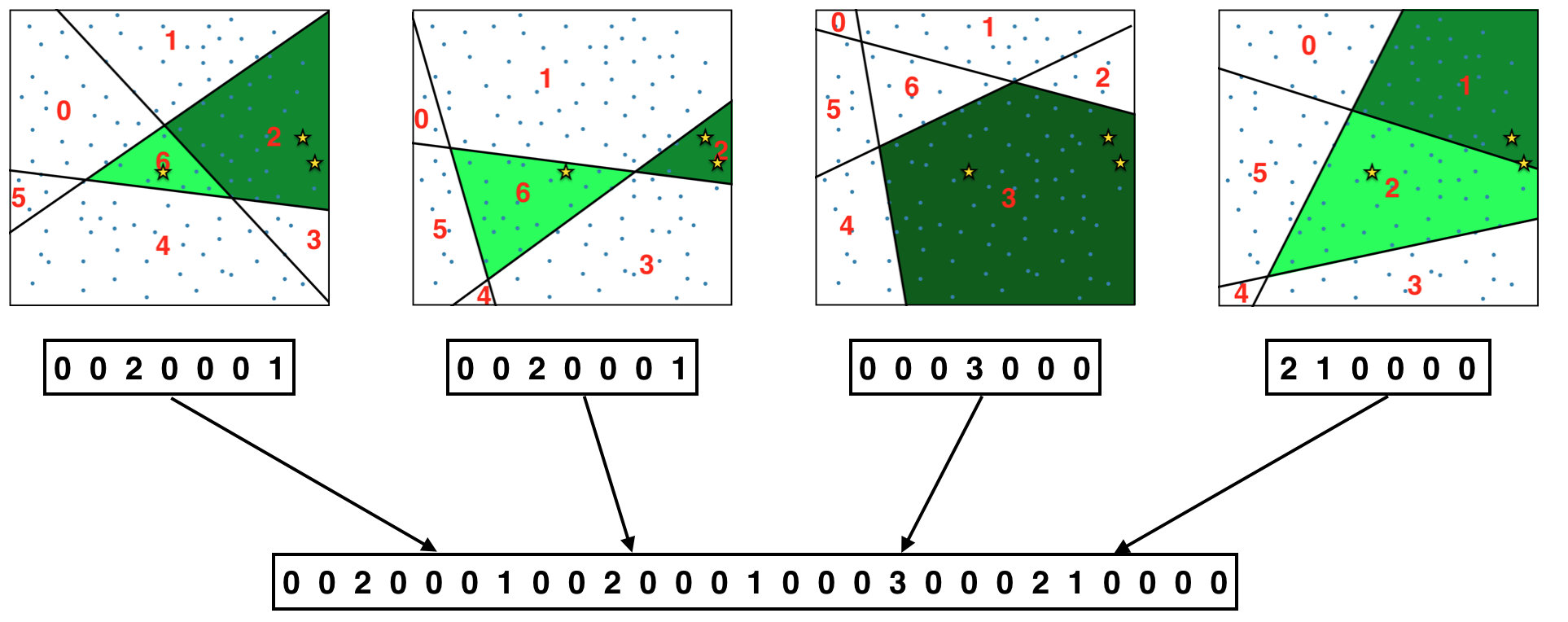
실제 임베딩 표현은
[0, 0, 2, 0, 0, 0, 1, 0, 0, 2, 0, 0, 0, 1, 0, 0, 0, 3, 0, 0, 0, 2, 1, 0, 0, 0, 0]
이런 임베딩 표현을, Sketch라고 부르는데, 이 스케치는 만드는 과정에서 확인할 수 있듯 Addtive하다. sketch({apple, salami}) = sketch({apple}) + sketch({salami}).