잡담
회사 내에서 엔지니어가 아닌 사람에게 공유하기 위해 만든 글입니다. 이 주제에 관심 있는 사람에게 도움이 될 것 같아 공유합니다.
개요
이제 인터넷 어디에서나 추천 시스템을 찾아볼 수 있다. 추천 시스템이라는 말을 들어보지 못한 사람은 많겠지만, 밑의 예시를 보면 ㅇㅎㅇㅎ 하고 바로 알 것 같아서 추천 시스템에 대한 자세한 설명은 하지 않겠다.
추천 시스템은 보통 이런 일을 한다.

쿠팡에서 내가 전에 봤던 아이템과 비슷한 아이템을 추천해준다. (Finding similar items)
유투브가 내가 좋아할 만한 동영상을 추천해준다. (Recommendation)

구글 광고가 내가 예전에 봤던 물건과 비슷한 광고를 내게 보여준다(Contextual advertising, Retargeting)
추천 시스템과, Paradox of Choice
추천 시스템의 정의는 다양하지만, 내가 가장 좋아하는 추천 시스템의 정의는 다음과 같다.
추천 시스템은 검색 엔진의 검색 결과를 의도적으로 제한하는 방법이다.
정확한 인용은 아니며, 누가 이 말을 했는지 기억이 나지 않는다.
이 정의는 추천 시스템이 존재하는 가장 중요한 이유를 잘 요약해준다고 생각한다.
영화 대여점, 혹은 VOD 사이트에서, 무수히 많은 영화 포스터를 보며 무엇을 선택할지 고민해본 적이 다들 있을 것이라 생각한다. 혹은 인터넷에서 무언가를 사고자 할 때, 수많은 물건을 확인하느라, 심지어 내가 어떤 걸 맘에 들어했는지도 까먹어버린 경험은 다들 있을 것이다.

(The Paradox of Choice에 대한 좋은 포스트)
이는 Paradox of Choice 라고 하는 현상이다. 선택지가 많아질 수록, (1) 선택을 하는 비용의 증가, (2) 기회 비용에 대한 매몰 비용 등으로 인해 만족도가 감소하는 현상을 말한다.
추천 시스템은 이 문제를 해결하는 훌륭한 방법이며, 유저가 확인할 수 있는 결과를 제한함으로서 위의 문제를 해결한다. 즉, 유저가 수많은 아이템을 비교하고 결정하는 비용을 없애면서도, 유저의 만족도는 (유저가 모든 선택지를 고려했을 때와 비교하여) 높은 채로 유지시키는 것이 추천 시스템의 목표이다. 추천 시스템은 기본적으로 유저가 좋아할 만한 아이템만 잘 남기고, 유저가 좋아하지 않을 것 같은 아이템을 필터링하려고 노력한다. 사실 실제 추천 모델의 성능은 Clickthrough Rate, Conversion Rate를 높이는 것으로 평가하지만, 높아진 CTR은 유저가 선호할 만한 아이템을 빨리 보여 준 결과일 것이다.
이 글에서는 추천 시스템이 어떻게 유저가 좋아할 만한 아이템을 선택하는가와, 유저가 좋아하는 아이템을 선택하는 방법이 가져오는 문제에 대해 간단히 다룰 것이다.
추천 시스템은 유저의 행동 자체에 영향을 미친다.
[machines] mediate more and more of what we do. They Guide an increasing proportion of our choices - where to eat, where to sleep, who to sleep with and what to read. From Google to Yelp to Facebook, they help shape what we know.
[기계는] 점점 우리의 선택을 점점 더 많이 결정한다. 어디서 무엇을 먹는가, 어디에서 자는가, 누구랑 잠을 같이 자는가, 혹은 무엇을 읽는가까지. 구글, 옐프(식당 추천 서비스), 페이스북까지, 인터넷은 당신의 지식을 결정한다.
Eli Pariser The Filter Bubble의 저자, TED 강연자.
추천 시스템은 모델이 판단하기에, 유저가 좋아할 것 이라 생각하는 아이템을 선택해 유저에게 전달한다. 유저가 좋아할 만한 아이템을 찾는 방법에는 여러 가지가 있지만, 그 중 가장 쉬운 방법은 유명한 아이템을 추천해주는 것이다. 유명한 아이템을 유명하게 만드는 이유는, 그 아이템이 정말로 훌륭해서, 많은 사람들이 그 아이템을 좋아할 가능성이 높기 때문이다.
추천 시스템의 평가 방법도 이를 어느 정도는 장려한다. 추천 시스템을 평가하는 일반적인 방법은, “유저가 본 아이템을 얼마나 잘 맞추는가?”에 맞추어져 있다. Precision, Recall, MAE, Hold-out, k-fold cross validations…와 같은 대부분의 추천 시스템 평가 방식이 이러하다. 추천 시스템이 유명한 아이템을 얼마나 자주 추천하는가에 관한 문제는 고려하지 않는다. 모델이 어떻게 구성되어 있는지(단순한 popularity based recommendation에서 시작해서, Matrix Factorization, Autoencoder, RNN에 이르기까지)와는 그리 상관 없이, 추천 시스템은 유명한 아이템을 더 많이 추천하는 경향이 있다.
많은 Collaborative Filtering Model의 경우, 유명한 아이템 은 interaction이 많아, 더 정확한 예측값을 만들 수 있다고 생각해 더 많이 추천되는 경향이 있지만, 유명한 아이템을 얼마나 추천하는가는 트레이닝 과정에서 신경을 쓰지 않는다. 즉, 추천 시스템은 유명한 아이템을 자주 추천하게 된다.

이 그래프가 마케팅, 추천 시스템 업계에서 많이 사용되지만, 원래 의미는 다음과 같다고 생각한다. long-tail에도 많은 기회가 있지만, 결국 가장 많은 사람의 관심을 받으며, 가장 많이 팔리는 것은 소수의 좋은 아이템들이며, 이들이 유명해지는 것이다.
하지만, 유명한 아이템을 추천하는 경우 추천 시스템의 존재 가치가 조금 퇴색되는 경향이 있는 것 같다. 적어도, 유저가 이미 알고 있는 아이템을 추천하는게 추천으로서의 큰 의미가 있을까?
현재 추천 시스템의 평가 방법은, “유저가 본 아이템을 얼마나 잘 맞추는가?”(Precision, Recall, MAE, Hold-out, k-fold cross validations…와 같은 대부분의 추천 시스템 평가 방식)에 맞추어져 있고, 유명한 아이템을 얼마나 추천하는가에 관한 문제는 전혀 고려하지 않는다. 즉, 추천 시스템은 유명한 아이템을 자주 추천하게 된다.
추천 시스템은 유저의 행동 자체에 영향을 미친다. 정확도에만 집중하는 추천 시스템은 유명한 아이템 위주의 추천을 만들고, 이 점이 만드는 문제는 다음과 같다.
Accuracy에만 집중한 추천 시스템은
- 유저가 좋아할 만한 아이템을 골라 몇 개를 추천한다.
- 유명한 아이템이 선택될 가능성이 높다.
- 유명한 것 자체는 아이템의 Quality의 indicator이므로, 좋은 아이템일 가능성은 높지만…
- 또한, 유저가 이미 알고있는 아이템을 추천할 확률이 높아진다.
- User의 view history에 유명한 아이템이 더 추가된다.
- 추천 시스템은 기본적으로 유저의 view history 를 기반으로 아이템을 추천한다.
- 결국 추천 시스템은 다시 유명한 아이템을 추천하게 된다.
이 효과는 Rich-Get-Richer Effect라는 이름으로 알려져 있으며, 기업의 수익과, 유저의 만족도 양쪽 측면에서 악영향을 미친다.
Rich-get-Richer Effect
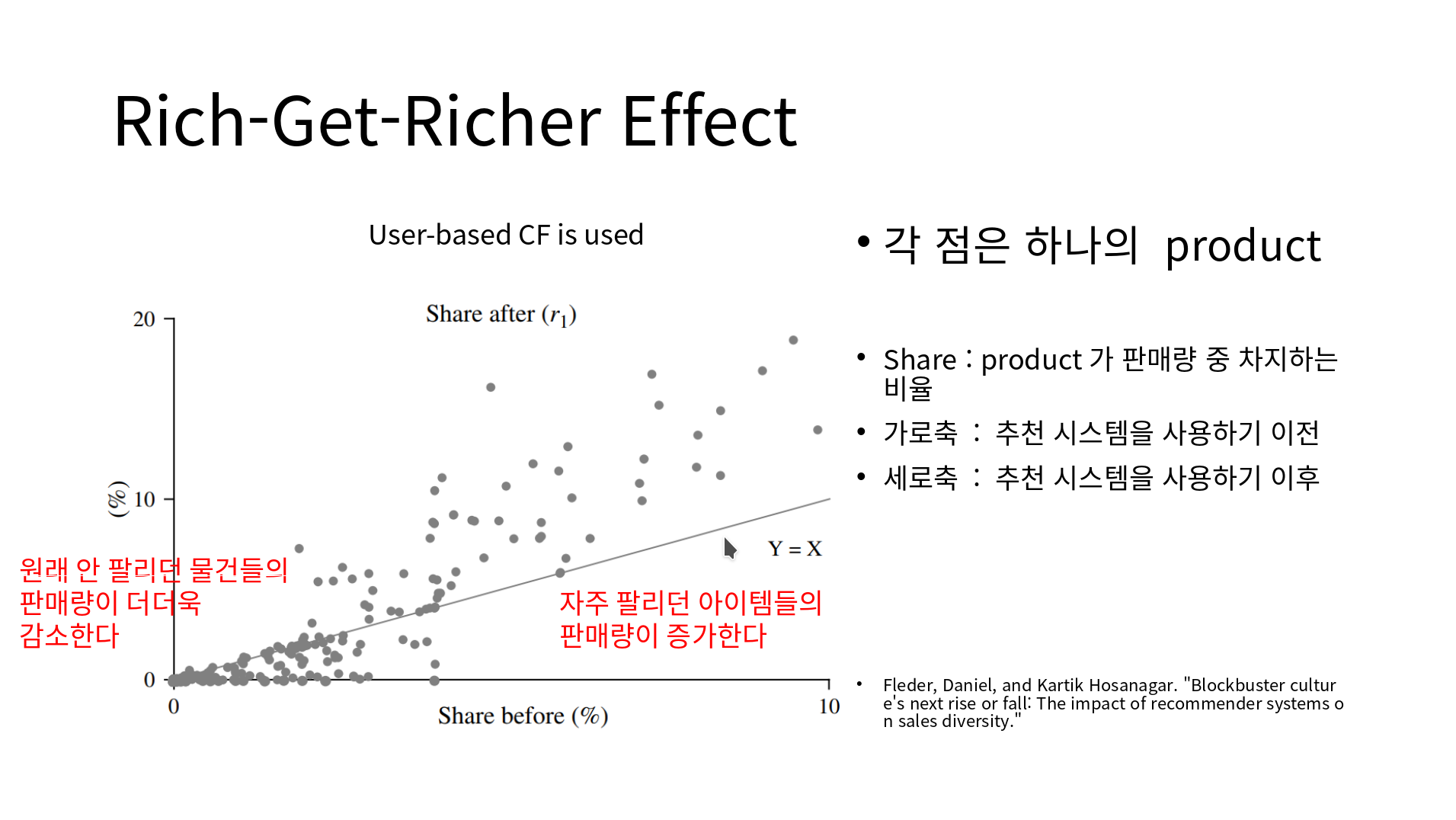
위 표는 어떤 추천 시스템을 사용하는 인터넷 쇼핑 몰의 판매량 데이터이다. 추천 시스템을 적용한 후, 유명한 아이템이 더 추천이 많이 되고, 유명한 아이템의 판매량이 증가한다. 하지만, 유명하지 않은 아이템의 경우 추천 시스템이 적용된 이후 판매량이 감소한다. 이 효과는 추천 시스템을 도입하며 기대했던 효과인 판매량의 증가가, 적어도 일부 아이템에 대해서는 일어나지 않는다는 증거이다.
다양성의 부족이 유저의 만족도를 해치는 실제 예시
다양성의 감소로 인해 유저의 만족도를 낮추는 사례는 많다. 하지만 아무래도 실제로 경험한 일을 얘기하는게 좋을 것 같다.
나는 별 일이 없으면 항상 유투브 레드로 음악을 듣고 있다. Youtube Red는 음악 한 곡을 들으면 자동으로 다음에 들을 음악을 정하고(추천), 이를 재생한다. 이때, 다음에 들을 음악은 현재 듣고있는 음악과 비슷한 음악이 선택된다.
즉, 음악 A를 들은 이후에 A와 닮은 음악 B가 재생되고, B 음악의 이후에는 B와 닮은 음악 C가 재생된다. 이렇게, 음악이 자동적으로 [A ,B, C, D, E, …, K] 이어진다. 문제점은, A, B,C, …, K까지의 음악이 서로 모두 비슷하다는 점이다.. 몇 번의 음악 추천이 지나면(K) 다음 추천되는 음악은 K와 비슷한 A가 재생(추천)된다. A의 다음에는 다시 B가 재생되고,… 이런 Loop가 생기게 되어, 새로운 음악을 듣지 못하게 된다.
이 결과를 받아들인다면, 추천 시스템이 해야할 일은 다음과 같아진다.
- 추천 시스템은 유저가 좋아할 만한(Relevant to request)한 아이템을 추천해야 한다.
- 그와 동시에, 추천 시스템은 다양한 아이템을 추천해주어야만 한다.
추천 시스템에서 사용할 수 있는 Diversity Metrics
Make it measurable
당연하지만, 측정할 수 없는 것은 관리할 수 없고, 관리할 수 없는 것은 개선할 수도 없다. 추천 시스템의 다양성을 측정할 수 있는 간단한 방법에 대해서 알아보자.
예시 1
어떤 학생이 공부를 잘 하고 싶으면, 우선 해야 할 일은 자신의 수준을 잘 알아야 한다. 이 때 일반적으로 사용되는 metric은 시험 성적이다. 실제로 측정하기 힘든 기준인 공부 실력 을 시험 성적 을 통해 측정이 가능하게 바꿔야 한다. 이 경우 시험 성적 이 학생의 공부 실력에 대한 metric이다.
Metric에 대해 아주 formal한 정의는 하지 않을 것이다.(나도 잘 모르기 때문이다…) 다만, Metric이 가져야 하는 간단한 특징에 대해 알아보는 것은 의미가 있을 것 같다. 사실 이는 아주 당연한 얘기이다.
- 우리가 기대하는 목표를 반영해야 한다.
- 성적이 높은 학생이, 더 공부를 잘 할 것이라는 기대를 갖고 시험 성적을 활용하기로 결정했으면, 실제로 성적이 높은 학생이 공부를 더 잘 해야 한다.
- 하지만, 실제 기준과 거리가 있을 수도 있다. 어떤 학생은 시험기간만 되면 긴장해서 자신의 실력을 100% 발휘할 수 없을 수도 있다.
- 비교가 가능해야 한다 (따라서, 숫자로 나타내야 할 수도 있다.)
- 어떤 학생이 90점을 맞고, 다른 학생은 80점을 맞는다. 그럼 90점 받은 학생이 공부를 더 잘 한다고 말할 수 있을 것이다.
- 즉, A > B라는 식으로 표현이 가능해야 한다.
예시 2
아주 간단한 Linear Regression Model을 생각해 보자.
Linear Regeression Model(이하 모델)을 만들 때, 우리는 모델이 $x_k$를 입력으로 받았을 때, 실제 $y_k$값과 비슷한 $\hat{y_k}$값을 생성하기를 기대한다.
즉, 이게 우리가 모델에개 기대하는 것이다. 모델을 평가하기 위해 사용하는 방법 중 MAE라는 Metric이 있다. 정의는 다음과 같다.
\[\text{MAE} := \frac{1}{n}\sum_{i}^{n}{ \mid y_i-\hat{y_i} \mid }\]MAE가 방금 확인한 metric의 기준에 맞는지 간단히 확인해보자.
- 우리가 기대하는 목표를 반영해야 한다.
- 정의 자체 상, 실제 $y_k$값과 $\hat{y}_k$값이 비슷할 수록 MAE는 적어진다.
- MAE가 낮을 수록, 모델이 더 정확하다고 생각할 수 있다.
- MAE는 실수이다. 즉, 두 모델이 다른 MAE를 갖는 경우, 더 낮은 MAE를 갖는 모델을 선택할 수 있다.
따라서, MAE는 Linear Regression Model의 성능을 측정하기에 적합한 metric이다. 물론 MAE 이외에도 다양한 방법이 있다. RMSE도 있고, 생각나지 않지만 아주아주 많다. 이는 음… 아까 말한 문제중 하나이다. 기대하는 목표를 반영하고 있는 metric은 아주 많다. 더 좋은 metric을 정하는 방법은 생각보다 아주아주 어려운 일이다. 이에 대한 자세한 설명은 넘어가자.
이제, 추천 시스템에서 사용할 수 있는 Diversity Metric에 대해 “아주 간단히” 알아보자.
Sample data는 다음과 같다.
| 82년생 김지영 | 베이지안 계량경제학 | 송민령의 뇌과학 연구소 | 여고생 생태도감 | |
| 실제 유저의 클릭수의 합 | 10 | 12 | 33 | 8 |
| A 모델이 추천한 횟수 | 3 | 5 | 2 | 8 |
| B 모델이 추천한 횟수 | 3 | 3 | 3 | 3 |
| C 모델이 추천한 횟수 | 0 | 0 | 0 | 10 |
Coverage
Coverage는 전체 아이템 중 추천 모델이 추천에 사용한 아이템의 비율을 말한다. A 모델과 B 모델은 전체 아이템을 추천에 모두 이용했으므로, Coverage가 1이다. C 모델은 4가지 아이템 중 1가지 아이템만 추천에 이용했으므로, Coverage는 $1/4 = 0.25$이다.
Coverage는 간단하게 모델의 diversity를 확인할 수 있지만, A 모델과 B 모델과 같은 경우를 비교할 수 없다는 단점이 있다.
한눈에 보기에도, B 모델이 아이템을 더 균등하게 추천한다. 하지만, 두 모델의 Coverage는 동일하다. 이러한 문제를 어떻게 해결할까?
Entropy
예시
내가 지갑을 방 어딘가에 두고 까먹었다. 내가 지갑을 둘 만한 장소는 다음과 같다.
A = {책상 위, 침대 위} B = {책상 위, 침대 위, 바지 속, 세탁기 위} (단, 모든 장소에 지갑이 존재할 확률은 동일하다)
A, B 중 어떤 세계가 어느 세계에서 내가 지갑을 더 찾기 쉬운가? 당연히 답은 A이다. Entropy는 어떤 환경이 얼마나 정돈되어 있는지, 혹은 혼란스러운지를 측정하는 지표이다. 경우의 수가 다양할 수록 엔트로피가 높다. 경우의 수가 다양하지 않을 수록 엔트로피가 낮다. 많다, 적다라는 표현을 사용하지 않고 다양하다라는 단어를 사용한 이유는 Entropy는 경우의 수가 아니라(Coverage와는 달리) 그 사건(경우)가 발생할 확률도 함께 고려하기 때문이다.
물리학에서는 주로 분자 분포를 묘사할 때 엔트로피를 사용한다. 고체는 분자끼리 뭉쳐 있고, 분자가 존재할 위치가 기체일 때에 비해 비교적 정해져 있다. 따라서 기체일 때보다 고체일 때의 엔트로피가 더 낮다. 통계학에서는 일어날 수 있는 사건의 다양성을 묘사할 때 엔트로피를 사용한다.
추천 시스템을 평가할 때에는 아이템의 다양성과, 얼마나 많은 아이템이 균등되게 추천되는지 다양성을 묘사하기 위해 이용할 수 있다.
엔트로피의 정의는 다음과 같다.
\[\text{Entropy}(P) := - \sum_{i}{p_i \log (p_i)}\]$p_i$는 개별 아이템이 추천될 확률이고, 추천 모델이 개별 아이템 i를 추천할 확률은 $n_i / \sum_i{n_i}$으로 정의한다.
| 82년생 김지영 | 베이지안 계량경제학 | 송민령의 뇌과학 연구소 | 여고생 생태도감 | |
| 실제 유저의 클릭수의 합 | 10 | 12 | 33 | 8 |
| A 모델이 추천한 횟수 | 3 | 5 | 2 | 8 |
| B 모델이 추천한 횟수 | 3 | 3 | 3 | 3 |
| C 모델이 추천한 횟수 | 0 | 0 | 0 | 10 |
다시 toy data로 돌아가, 각 모델의 Entropy를 계산해 보자.
\[\text{Entropy}(A) = -[(3/18)\log(3/18)+(5/18)\log(5/18)+(2/18)\log(2/18)+(8/18)\log(8/18)] = 0.54\] \[\text{Entropy}(B) = -[(3/12)\log(3/12)+(3/12)\log(3/12)+(3/12)\log(3/12)+(3/12)\log(3/12)] = 0.60\] \[\text{Entropy}(C) = -[0 + 0 + 0 + 0] = 0\]Entropy를 기준으로 했을 때, B 모델이 A, C 모델보다 다양성이 더 높다고 말할 수 있다.
다만, 여기서 궁금해지는 점은 다음과 같다. 실제 유저의 클릭수(아이템의 클릭 분포)보다 더 다양한 아이템을 추천하는 것이, 정말 의미있을까?
위에서 얘기했듯이, 유명한 아이템에겐 각각 유명한 이유가 존재한다. 다양성이 중요하긴 하지만, 인사이드 아웃 과 오! 인천을 비슷한 빈도로 추천하는 추천 시스템은 분명 좋은 추천 시스템은 아닐 것이라 생각한다.
Relative Entropy, or KL divergence
간단히 생각할 수 있는 아이디어는 다음과 같다. 추천 결과의 아이템 분포는 유저의 아이템 클릭 분포와 비슷해야 하지 않을까? 추천이 원래 빈도와 비슷하다면, 인사이드 아웃이 추천되는 비율은 유저가 인사이드 아웃을 클릭하는 비율과 비슷할 것이다.
KL divergence는 두 확률 분포를 비교하는 방법이다. 두 확률 분포의 확률이 비슷하다면, KL divergence의 값이 작을 것이다.
정의는 다음과 같다. \(KL(P \mid Q) := \sum_i{p_i}\log(\frac{p_i}{q_i}) = -\text{Entropy}(P) + \text{Entropy}(P \mid Q)\)
계산은 살짝 번거로우니 결과만 보여주면 다음과 같다.
\[KL(A \mid O) := 0.21\] \[KL(B \mid O) := 0.07\] \[KL(C \mid O) := 0.89\]KL divergence가 가장 작은 B번 모델이 실제 아이템 클릭 분포와 가장 비슷하므로 B 모델이 가장 적절한 추천을 생성한다고 생각할 수 있다. 예시를 조금 잘못 만들긴 했는데 음… 원래는 A가 더 적합하게 나오는 예시를 만들어야 했는데 음음… 암튼, 이렇게 모델의 다양성을 평가할 수도 있다.
이외에도 diversity를 측정하기 위한 더 많은 방법이 있다.(참고)
결론
추천 시스템은, 정보 과잉을 해결하고, 유저의 Loyalty를 높이기 위해 사용되는 아주 좋은 도구이다. 추천 시스템은 직접적으로는 유저의 선택에 영향을 미쳐, 장기적으로는 유저의 행동과, 사이트의 수익에 직접적으로 영향을 미친다. 유저가 좋아할 만한 아이템을 맞추려는 시도(Accuracy)에만 집중한 추천 모델은 해로울 수 있다. Accuracy 이외에도 고려하면 좋을 지표가 많고, 그 중 하나로 Diversity에 대해 간단히 알아봤다. 물론 Diversity 이외에도 고려하면 좋을 만한 metric들도 많다.
바쁜 사람을 위한 3줄요약
- 추천 시스템은 큐레이션 이라는 정보 과잉을 해결하는 도구로 사용되고 있다.
- 검색 결과를 필터링하는 과정에서 검색 결과의 다양성이 저하되는 문제가 생긴다.
- 추천 시스템을 평가할 때, 추천의 정확도만이 아니라, 추천의 다양성도 함께 평가하면 좋을 것 같다.
…다음 글은 실제로 추천 시스템의 다양성을 향상시키기 위한 방법에 대해 알아보도록 하자.
References
-Fleder, Daniel, and Kartik Hosanagar. “Blockbuster culture’s next rise or fall: The impact of recommender systems on sales diversity.”
- Matevz Kunaver, Tmaz Pozrl. “Diversity in recommender systems – A survey.”, Knowledge-Based Systems Volume 123, 1 May 2017, Pages 154-162
- Pablo Castells et al. “Novelty and Diversity Metrics for Recommender Systems: Choice, Discovery and Relevance”