들어가며
이해의 목적으로, 내가 쓴 글을 남이 본다고 할 때 별 도움은 안되는 것 같다. 내가 이런 글을 쓰는 목적이 다른 사람을 이해시키려고 하는 게 아니기도 하고.. 이해를 정말 잘 해보고자 한다면, 분명 더 좋은 사람이 있을 거 같고, 별로 새롭거나 참신한 내용을 쓸 정도로 내가 전문가도 아니당.
Graph Representation Learning Book의 일부 챕터에 대한 요약이고, 내가 중요하게 생각하거나 이해를 못한 부분이 당연히 강조되어 있다.
Prerequiste;
\(G = (V, E, X_v, X_e)\), \(v \in V = \{1, 2, \dots, n\}\), \(e \in E \subseteq V \times V\), \(x_e \in R^{d_e}~~\forall e \in E, x_v \in R^{d_v} ~\forall e \in V\)
이런 노테이션을 쓴다. $E$에 corrsponding Adjacency Matrix는 $A$로 적는다. node feautres, edge features는 각각 $x_v, x_e$로 나타낸다.
Permutation Invariant
$v = {v_1, v_2, v_3}$인 그래프 $G$가 있다고 하자. 임의의 $d_v * m$, $(m \geq n)$인 MLP를 이용해서 node features를 전부 concat하고, 남는 공간은 zero-padding을 해서 그래프를 표현하는 방법이 있다고 해 보자. 이 함수의 문제점은, 같은 그래프에 대한 표현이 여러 개 있을 수 있다는 점이다. Concat은 $[v_1, v_2, v_3]$과 $[v_2, v_1, v_3]$의 결과가 다르다. 그래서, 두 입력이 같은 출력을 만든다는 보장이 없다. 실제로는 저 둘은 같은 그래프임에도 불구하고.
Adjacency Matrix $A$의 어떤 Permutation P으로의 변환 $PAP^T$는 모두 A와 같은 그래프를 나타낸다. 즉, 다음과 같은 성질을 만족하는게 좋다.
\[f(PAP^T) = f(A)\]이런 성질을 유지하는 딥러닝 모델을 조금 신경써서 만들어야 한다. 주로 이런 요소는, array적 요소 때문에 생긴다. node, edge를 set/aggregation으로 처리하면 일반적으로 이런 일이 안 생길 것이다.
Neural Message Passing
왜 이런 방식이 효과적이고, 어떤 직관으로 생겼는지는 아직 잘 이해를 못했다. 아무튼, 노드의 이웃들에게 자기 자신의 정보(message)를 propagate (or pass)하는 방식이 현재 가장 많이 쓰인다.
노드의 latent representation을 다음과 같이 정의한다.
\[h^{(0)}_v = x_v\]$\mathcal{N}(i)$는 node $v_i$의 이웃들의 집합. Neural Message Passing에서는 일반적으로, Neighbor에 자기 자신을 포함한다. 같은 말의 다른 표현으로는, graph에 self-loop를 더하는 것이 일반적이므로, 앞으로 자기 자신을 $\mathcal{N}(i)$에는 $v_i$도 포함한다고 정의하자. node의 표현은 다음과 같은 규칙으로 반복적으로 업데이트된다.
\[h^{(t+1)}_i = \text{Update}(\text{Aggregate}(\{h^{(t)}_j \vert j \in \mathcal{N}(i)))\]딥러닝을 쓴다고 하면, $\text{Update}$와 $\text{Aggregate}$가 Parameterized function이다.
위에서 말한 대로, $\text{Aggregate}$ 함수가 Permutation invariant한 것이 중요하다.
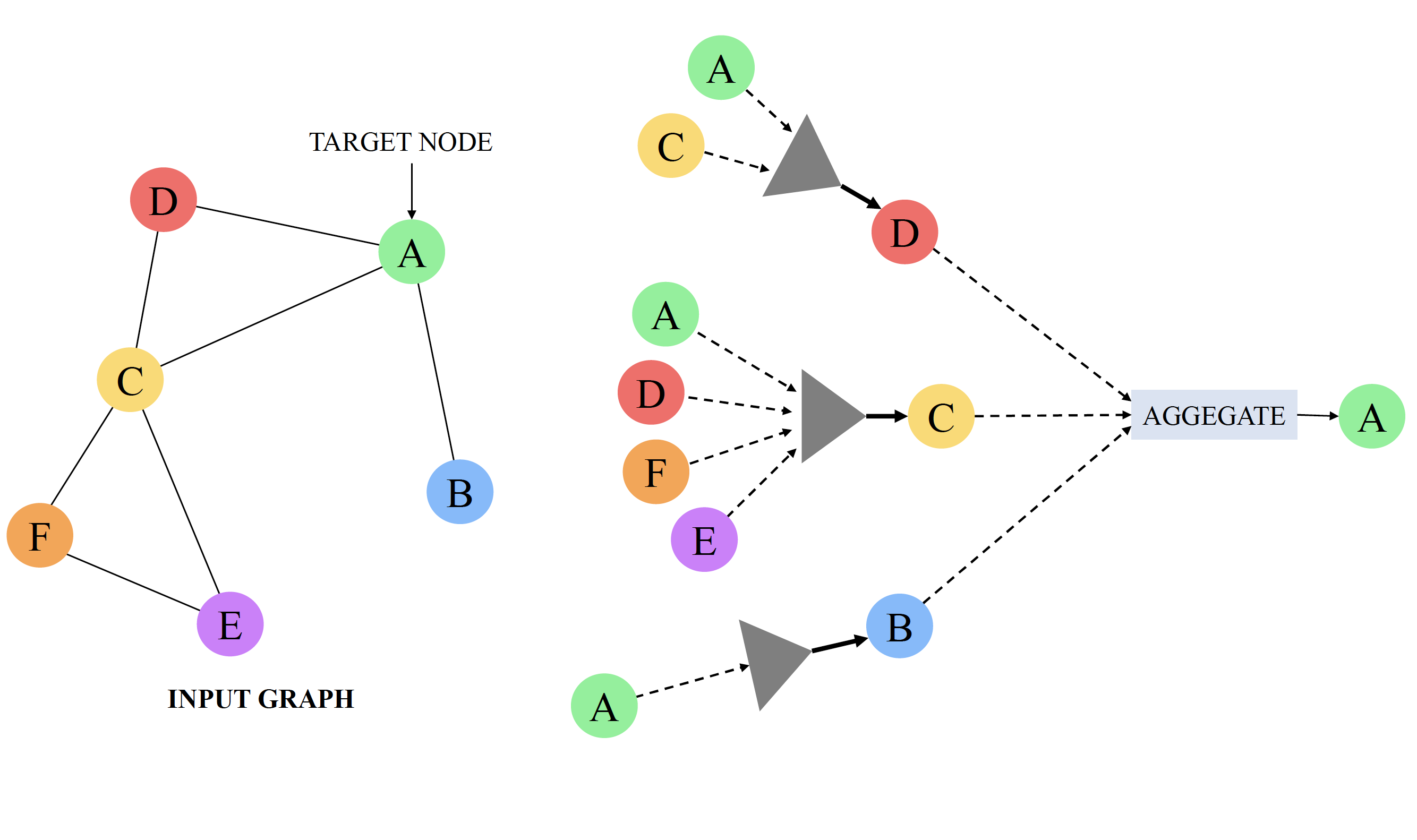대략 이런 형태로 표현이 생성된다. 우리는 이렇게 생성한 표현이 두 가지 정보를 (어떠한 방식으로든) 담기를 기대한다.
- Structual Information
- node $i$에 대한 임베딩을 만들 때, node들은 $i$와의 거리에 따라 각각 다른 iteration 단계에서 임베딩된다. 이런 과정에서, 그래프의 구조적 정보가 포함될 것이라 기대한다.
- Feature Information
- node의 표현은 결국 node의 feature를 기반으로 생성된다. 어떠한 방식으로든, 그 정보가 손실되지 않고 최종 표현에 담겨 있을 것이라 기대한다. 이는 RNN과 유사한 것 같다.
Aggregators
위의 Message Passing framework를 따른다고 할 때, 내 생각에 가장 중요한 것은 Aggregate 연산을 어떻게 정의할 지인 것 같다. 가장 생각하기 쉬운건 Sum/Averaging이다.
편의상 앞으로 \(\{h^{(t)}_j \vert j \in \mathcal{N}(i)\}\) 을 $H_\mathcal{N}(i)$이라 하자.
Sum or Average Aggregator
\(\text{Aggregate}() = \frac{1}{f(\mathcal{N}(i))}\sum h^{(t)}_j\) $f(X) = 1$ or $|X|$.
식의 유사성을 보면 알겠지만, 이 연산은 딥러닝 하는 다른 사람들은 보통 Pooling이라고 부른다. Permutation Invariant를 만족하는 다른 여러 조건들도 있을 수 있을 것 같다.
Set Pooling
\(\text{Aggregate}(H_\mathcal{N}(i)) = f(g(\sum_{h \in H_\mathcal{N}(i)}h))\) where $f, g$ is MLP.
이건 Sum, Mean을 포함하는 함수 공간을 모델링할 수 있어서, aggregation의 일반화라고 생각할 수 있을 것 같다.
Neighborhood Normalized Aggregator
\[\text{Aggregate}(H_\mathcal{N}(i)) = \sum \frac{h^{(t)}_j}{\sqrt{\mathcal{N}(i)\mathcal{N}(j)}}\]모든 node와 연결되어 있는 어떠한 node $v_g$가 있다면, 이 $v_g$가 전달하는 정보는 다른 node들을 구분하는 데에 전혀 도움이 되지 않을 것이라는 가정이 이 aggregation 방법에 숨어 있다. 이 aggregation의 가장 간단한 비유는 (내 생각에), 말이 너무 많은 사람은 별로 믿음직스럽지 못하다.인 것 같다. 이는 기존의 다른 ML on Graph(e.g., PageRank)에서도 비슷한 가정을 하고 있다.
Janossy Pooling
Permutation Invariant한 하나의 aggregator $f$를 만드는 대신, Permutation에 sensitive한 모델(주로 LSTM)을 이용해 많은 $\rho$를 만든 뒤에, 이를 averaging하는 방식이다.
\(\text{Aggregate}(H_\mathcal{N}(i)) = \frac{1}{\Pi}\sum_{\pi \in \Pi} \rho(\pi)\) where, $\pi$ is the ordered list of vertices.
만들 수 있는 permutation이 무지 크기에, 일반적으로 적당한 사이즈의 permutation을 샘플링해서 사용하거나, 혹은 Canonical ordering (DAG에서의 토플로지컬 소트와 같은) 순으로 정렬한 뒤, 생기는 tie (DAG를 topological sort하면 생길 수 있는 아웃풋이 여러가지)에 대해서만 averaging을 한다던가 하는 전략을 사용한다.
Attention과의 연관성.
또 나왔다. 어텐션. 내 생각인데, 이제 이 모듈은 Attentive Network라고 불러서 CNN이랑 RNN이랑 같은 취급을 해야 하지 않을까 싶다. 어텐션에 대한 설명은 생략한다. 이 글을 여기까지 읽은 사람이면 다들 알고있지 않을까? 사실 Transformer의 Attention의 가장 자연스러운 해석이 이러한 메세지 패싱이라고 생각한다.
\(\text{Aggregate}(H_\mathcal{N}(i)) = \sum \alpha_{ij} h^{(t)}_j\) where $\alpha_{ij}$ is attention score of $j$ to $i$.
자연스럽게, Gated Path, Skip-Connection, Jumping Connection같이 attention에서 자주 사용되는 테크닉들은, 여기서도 동일하게 쓰일 수 있다는 얘기다.
Edge Features
지금까지 얘기는 다 좋은데, node features만을 다뤘다. 근데 edge도 유용한 정보를 담는 경우가 많다. 최소한 방향이라도.
Finite edge features
edge의 종류가 $r$개 있다고 하자, edge type $k$의 neighbor는 $\mathcal{N}_k(j)$라 하자. 가장 단순하게는, 각각의 edge마다 다른 transformation을 해주는 것일 것이다.
\[\text{Aggregate}(H_\mathcal{N}(i)) = \sum_{k=1}^r \sum \frac{W_k h^{(t)}_j}{f_k(\mathcal{N}(i),\mathcal{N}(j))}\]Edge가 vector로 정의되는 특징을 가질 경우
이 책에서는 언급이 잘 없는 것 같다. Pytorch-geometric이라는 좋은 라이브러리에 구현체가 몇개 있다. NN-Conv
Edge 정보로 Weight을 만들어주거나,
def message(self, x_j: Tensor, edge_attr: Tensor) -> Tensor:
weight = self.nn(edge_attr)
weight = weight.view(-1, self.in_channels_l, self.out_channels)
return torch.matmul(x_j.unsqueeze(1), weight).squeeze(1)
GENCONV
def message(self, x_j: Tensor, edge_attr: OptTensor) -> Tensor:
msg = x_j if edge_attr is None else x_j + edge_attr
return F.relu(msg) + self.eps
Node features로 임베딩을 시켜주거나 한다.
Graph Pooling
메세지 패싱은 node에 대한 표현밖에 만들지 않는다. 그래프에 대한 연산을 하고싶은 경우, Node level의 features를 Graph레벨의 summarization으로 바꾸는 Aggregation이 필요하다. 위에서 aggregation하는 방식과 역시 비슷한 방법이 쓰인다. 다만, 그래프 레벨에서는 neighbor 관계가 명확하지 않으니 set 전체에 대한 연산을 하거나 한다.
edge에 대한 표현은 왜 없냐고 생각하는 경우도 있을 텐데, 사실 임의의 그래프는 Edge, Node를 서로 flip해서 바꿔줄 수 있다. 그래프를 만들 때, 그냥 내가 더 중요하다고 생각하는 걸 node로 표현하는 경우가 일반적이다.
라고 생각했었는데, edge representation을 만들 수 있는 방법도 필요한 것 같다. Node 정보도 필요하고, edge 정보도 동시에 필요할 수도 있다. 이런 경우, 위의 과정을 Edge를 마치 node처럼 생각해 이터레이션을 돌고, node를 마치 edge처럼 생각해 이터레이션을 돌고, 이렇게 Alternating하는 방식을 생각해 볼 수 있겠다. 이런 생각을 처음 한 사람은 어떤 천재일까…?
잡담
재밌는 얘기는 사실 더 뒤에 나온다. 왜 이런 구조가 자연스러운지 뭐 이런 것들.